Giải chi tiết bài tập dao động: Quãng đường và thời gian trong dao động điều hòa

1 Bài tập dao động: Quãng đường và thời gian trong dao động điều hòa

Hãy bấm vào đây để xem đề: BÀI TẬP DAO ĐỘNG: QUÃNG ĐƯỜNG VÀ THỜI GIAN TRONG DAO ĐỘNG ĐIỀU HÒA.

2 Giải chi tiết bài tập dao động: Quãng đường và thời gian trong dao động điều hòa

Câu 1 . Công thức liên hệ chu kì, tần số và tần số góc

Đáp án B

\begin{align} \omega=\frac{2\pi}{T}=2\pi f \end{align}

Câu 2 . Định nghĩa tần số trong dao động điều hòa

Đáp án C

Câu 3 . Định nghĩa chu kì trong dao động điều hòa

Đáp án A

Câu 4 . Đơn vị của tần số góc

Đáp án D

Câu 5 . Cho phương trình dao động $x=10\cos{\left(6\pi t+\frac{5\pi}{6}\right)}$

a) Đáp án A

Trong phương trình dao động $x=A\cos{\left(\omega t+\varphi\right)}$, nếu $A\gt 0$ thì pha dao động là $\omega t+\varphi$.

b) Đáp án D

Quỹ đạo chuyển động được tính từ biên dương đến biên âm, nó bằng $2A$.

c) Đáp án A

Thời gian vật thực hiện được một dao động toàn phần là chu kì (bài toán đã cho tần số góc $\omega=6\pi\ \text{rad/s}$) \begin{align} T&=\frac{2\pi}{\omega}\\ &=\frac{2\pi}{6\pi}=\frac{1}{3}\ \text{s} \end{align}

d) Đáp án D

Vị trí và chiều chuyển động của chất điểm khi $t=0$ được xác định đồng thời bằng đường tròn pha. Ta phân tích như sau: Nói đến thời điểm ban đầu ($t=0$) ta phải xét đến pha ban đầu $\varphi=\frac{5\pi}{6}$, đây là tọa độ cung của điểm pha $P_0$ trên đường tròn pha. Hình chiếu $D_0$ của $P_0$ ở tọa độ $x_0=-\frac{\sqrt{3}}{2}A=\frac{\sqrt{3}}{2}10=-5\sqrt{3}\ \text{cm}$. Đây là vị trí.

Hình 1: Chú ý chất điểm dao động điều hòa là $D$ trên trục $Ox$, còn điểm $P$ trên đường tròn chỉ là một điểm ảo do chúng ta tưởng tượng ra để mô tả cho pha dao động mà thôi.

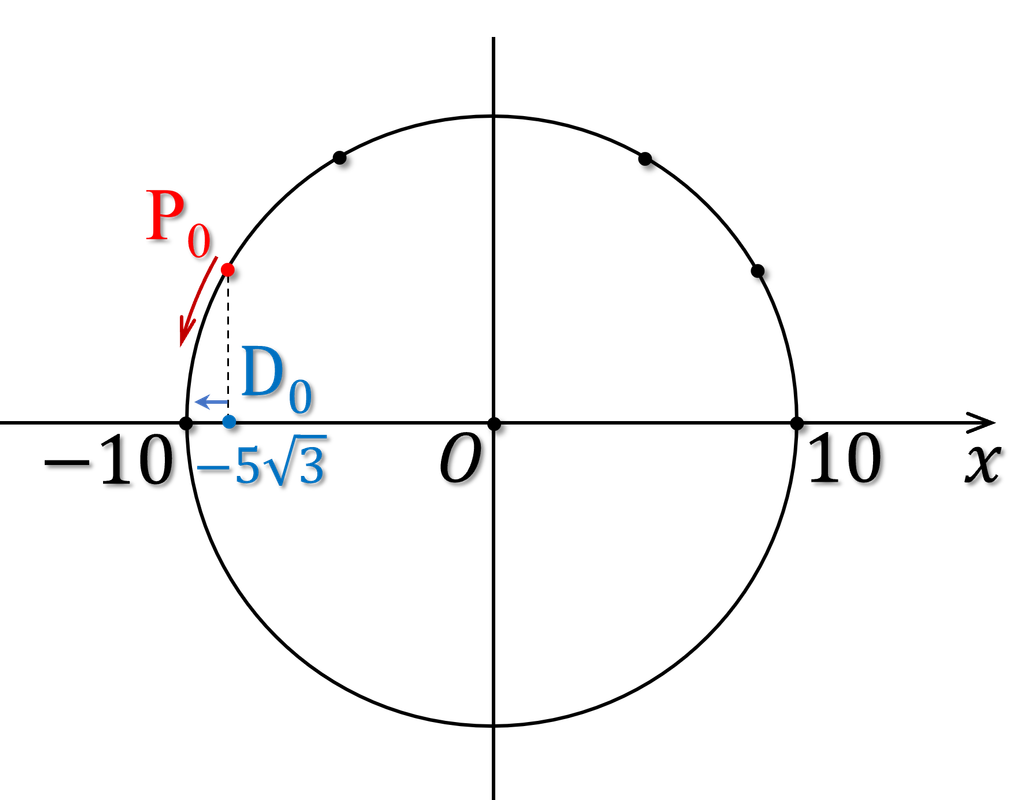
Về chiều chuyển động của chất điểm (vẫn chú ý rằng: Chất điểm dao động là điểm $D$ trên $Ox$), ta phải nhìn vào điểm pha $P$. Điểm $P$ luôn chuyển động ngược chiều kim đồng hồ (chiều lượng giác) nên khi $P$ ở phía trên trên so với $Ox$ thì nó đang đi sang trái. Mặt khác điểm $D$ luôn phải chuyển động cùng chiều $P$ như hình với bóng, nên $D$ cũng đang chuyển động sang trái. Ở đây người ta nói nó chuyển động ngược chiều $Ox$, tức là ngược chiều dương.

e) Đáp án C

Ta vẽ lại đường tròn pha như sau:

Hình 2: Khi chất điểm ở biên âm thì điểm pha $P_1$ cũng ở đó, khi nó đến vị trí có li độ $x_1=5\ \text{cm}$ thì điểm pha đến vị trí $P_2$.

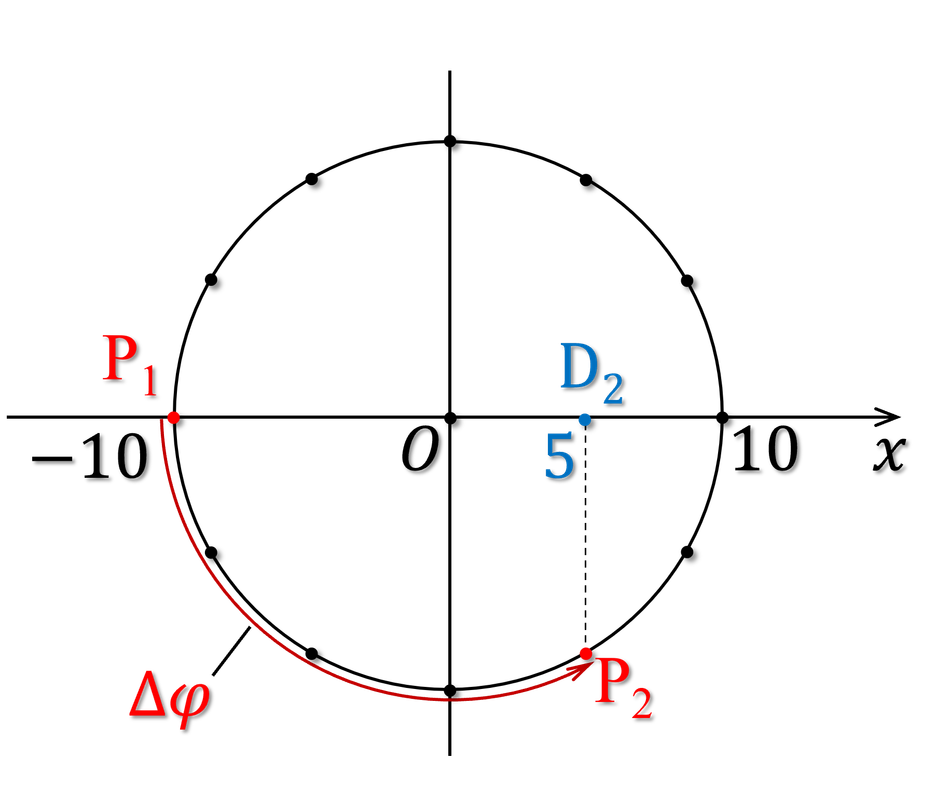
Đếm số cung $\frac{\pi}{6}$ trên đoạn $\Delta \varphi$ ta được \begin{align} \Delta \varphi=\frac{2\pi}{3} \end{align}

g) Đáp án B

Để tính được quãng đường đi của $D$, ta phải tìm cung di chuyển của $P$, nó là độ biến thiên pha \begin{align} \Delta \varphi&=\omega \Delta t\\ &=6\pi\times\frac{1}{12}=\frac{\pi}{2} \end{align} $\Delta \varphi=\frac{\pi}{2}$ bằng 3 đoạn cung $\frac{\pi}{6}$, ta vẽ trên đường tròn pha như dưới đây:

Hình 3: Ban đầu điểm pha là $P_0$ và chất điểm là $D_0$, sau thời gian $\Delta t=\frac{1}{12}\ \text{s}$ điểm pha đi được cung $\Delta \varphi=\frac{\pi}{3}$ đến điểm $P_3$, lúc đó chất điểm đã đến $D_2$.

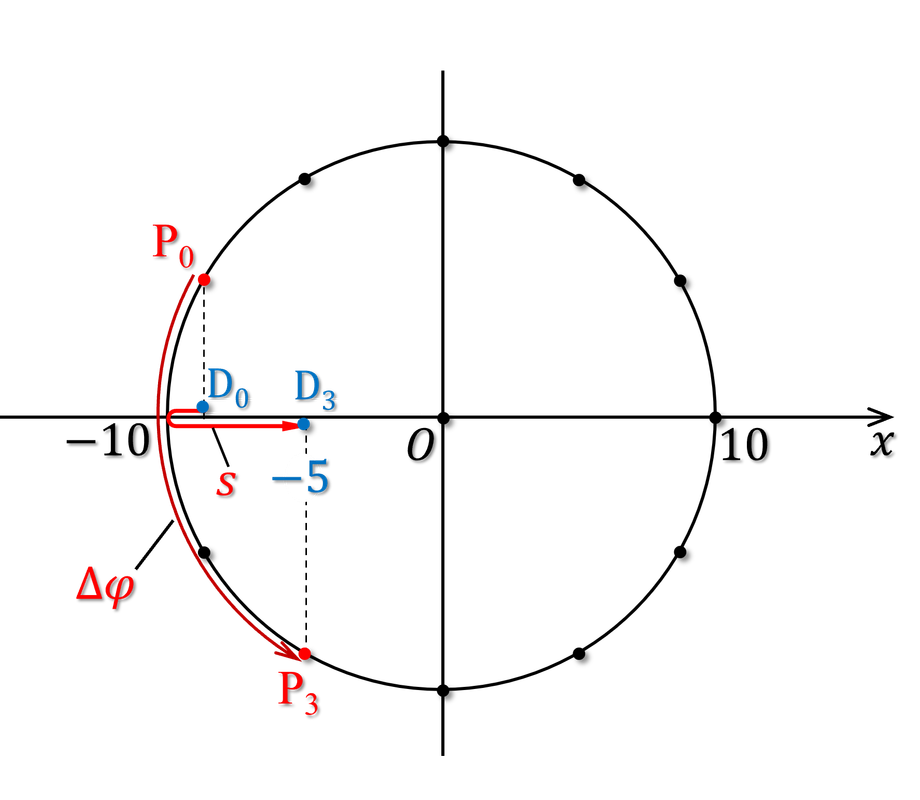
Quỹ đạo di chuyển của chất điểm $D$ trong thời gian này được vẽ bởi đường màu đỏ sát với $Ox$, nó chính là quãng đường của chất điểm, nó bằng đoạn từ $D_0$ đến biên âm cộng với đoạn từ biên âm đến $D_3$ \begin{align} s=10-5\sqrt{3}+5\approx6\text{,}34\ \text{cm} \end{align}

h) Đáp án A

Để tính thời gian $\Delta t$, ta phải vẽ đường tròn pha và xem xét điểm $P$ chạy một cung $\Delta \varphi$ bằng bao nhiêu, khi đó ta sẽ tính được thời gian bằng $\Delta t=\frac{\Delta \varphi}{\omega}$.
Mỗi chu kì (ứng với 1 vòng chạy của điểm pha $P$), chất điểm đi qua rồi đi lại điểm $x=5\sqrt{3}\ \text{cm}$, tức là đi qua hai lần, ứng với hai điểm 1 và 2 trên vòng tròn.

Hình 4: Ban đầu điểm pha là $P_0$ và chất điểm là $D_0$, cả $P$ và $D$ chạy 1 vòng ($2\pi$) thì $D$ đi qua $5\sqrt{3}$ hai lần ứng với vị trí (1) và (2) của $P$.

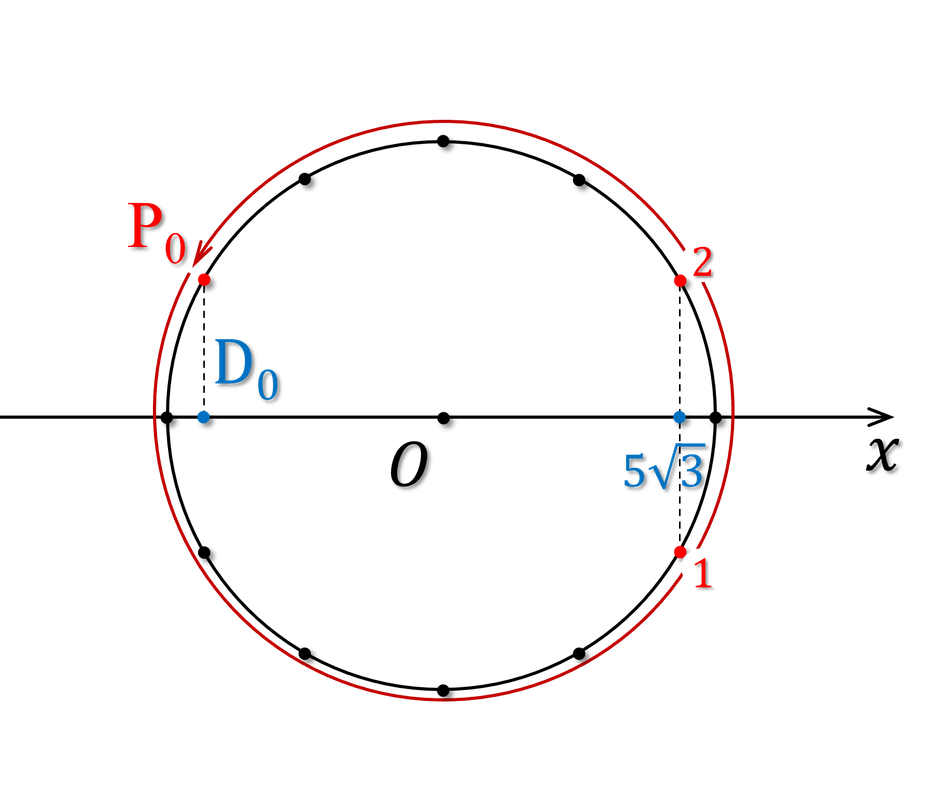
Bài toán yêu cầu $D$ đi qua $5\sqrt{3}$ lần thứ 2018 thì $P$ phải đi mấy vòng?
Nhiều bạn sẽ nói ngay là phải đi $\frac{2018}{2}$ vòng. Tuy nhiên như vậy thì hơi chủ quan. Các bạn nhìn hình 5 dưới đây để thấy:

Hình 5: Vòng cuối cùng điểm $P$ không cần chạy cả vòng, nó chỉ cần chạy tới điểm 2018 là đủ.

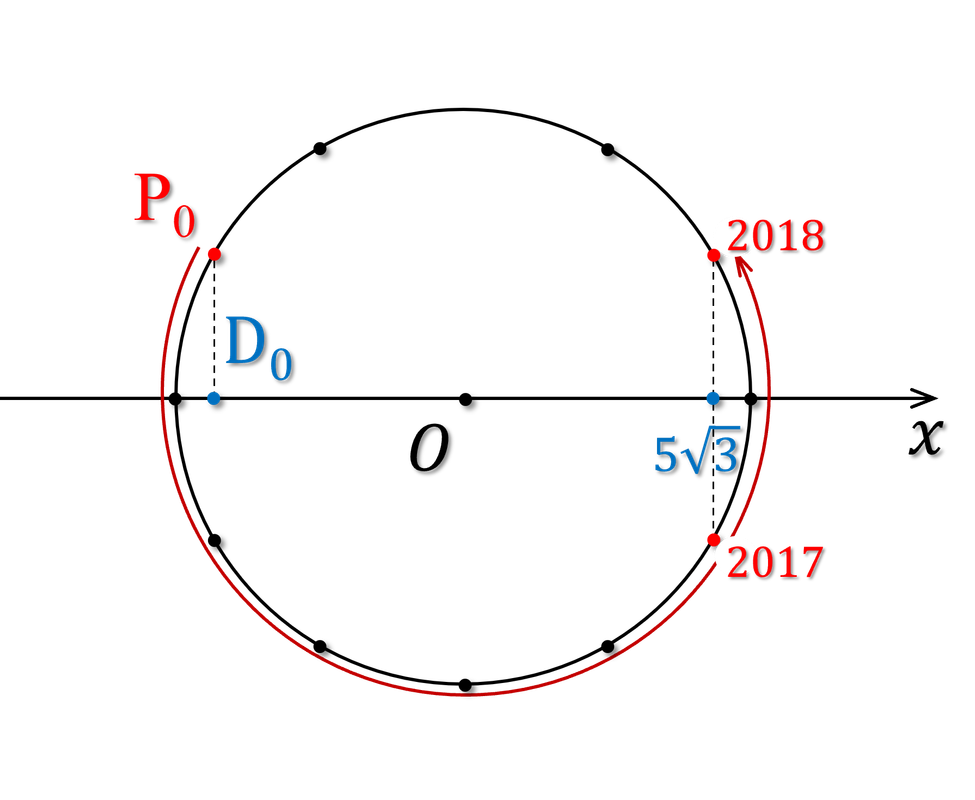
Điểm $P$ chỉ cần chạy $\frac{2018}{2}\ \text{vòng}$ bớt đi $3\frac{\pi}{6}$ là đủ. Mỗi vòng ứng với $2\pi$, vậy nên \begin{align} \Delta \varphi&=\frac{2018}{2}\times 2\pi-3\frac{\pi}{6}\\ &=2017\text{,}5\pi\\ \Delta t&=\frac{\Delta \varphi}{\omega}\\ &=\frac{2017\text{,}5\pi}{6\pi}=336\text{,}25\ \text{2} \end{align}

Câu 6 . Cho quãng đường đi từ thời điểm $t_0=0$ đến thời điểm $t_1$, tìm quãng đường đi từ thời điểm $t_1$ đến thời điểm $t_2$

Đáp án C

Cứ bài toán quãng đường hay thời gian, ta đều vẽ ngay đường tròn pha, không cần chần chừ gì cả. Vậy vẽ cái đường tròn rồi vẽ gì trên đó nữa?
Ta xem bài toán cho $\Delta t$ thì ta tính được $\Delta \varphi$ rồi vẽ $\Delta \varphi$ vào, từ $\Delta \varphi$ ta xác định được quãng đường $s$. Ngược lại nếu bài toán cho $s$ thì ta vẽ $s$ vào, rồi từ hình vẽ xác định được $\Delta \varphi$, khi đó ta tính được $\Delta t$.
Bài toán này cho ta gì nào! Họ cho $s_1$ và cả $\Delta t_{01}$, ta vẽ $s$ trên đường tròn:
+ Bài toán cho pha ban đầu $\varphi=\frac{\pi}{2}$, ta vẽ được điểm pha ban đầu $P_0$, từ đó vẽ được vị trí ban đầu $D_0$ của vật và chiều chuyển động của vật ban đầu (sang trái).
+ Vì biên độ $A=8\ \text{cm}$ nên quãng đường $s_1=4\ \text{cm}$ là một nửa biên độ, tức là cung $\overset{\huge\frown}{P_0P_1}=\Delta \varphi_{01}=\frac{\pi}{6}$

Hình 6: Vẽ quãng đường $s_1$ để suy ra $\Delta \varphi_{01}$ và suy ra $\omega$.

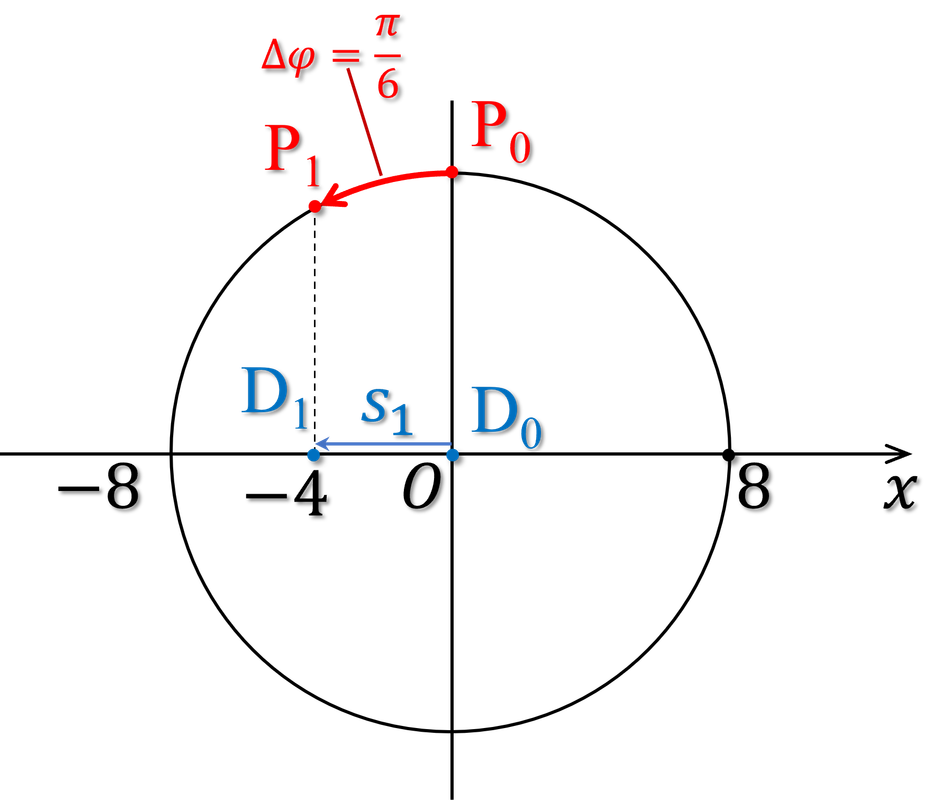
Suy ra tần số góc \begin{align} \omega&=\frac{\Delta\varphi_{01}}{\Delta t_{01}}\\ &=\frac{\frac{\pi}{6}}{0\text{,}5}=\frac{\pi}{3}\ \text{rad/s} \end{align} Bây giờ ta đã biết $\omega$, biết $\Delta t_{02}=12\text{,}5\ \text{s}$, ta suy ra $\Delta\varphi_{02}$, vẽ cung này ta sẽ suy ra quãng đường. \begin{align} \Delta\varphi_{02}&=\omega\Delta t_{02}\\ &=\frac{\pi}{3}\times 12\text{,}5\\ &=\frac{25\pi}{6}=4\pi+\frac{\pi}{6} \end{align} Tức là kể từ thời điểm ban đầu đến thời điểm $t_2$ vật đã đi được 2 vòng ($4\pi$) và thêm một cung $\frac{\pi}{6}$ như ở hình 6. Ta suy ra quãng đường \begin{align} s_2&=2\times 4A+s_1\\ &=2\times4\times8+4=68\ \text{cm} \end{align}

Câu 7 . Lập phương trình dao động

Đáp án C

Lập phương trình dao động thực ra là tìm biên độ $A$, tần số góc $\omega$ và pha ban đầu $\varphi_0$. Trước hết ta tính được $\omega$ từ chu kì $T$ \begin{align} \omega&=\frac{2\pi}{T}\\ &=\frac{2\pi}{1\text{,}8}=\frac{10\pi}{9}\ \text{rad/s} \end{align} Bài toán cho một khoảng thời gian có điểm đầu tại li đô 3 cm đang đi về vị trí cân bằng, tức là đi sang trái, đến điểm cuối là biên, ứng với \begin{align} \Delta \varphi&=\omega\Delta t\\ &=\frac{10\pi}{9}\times0\text{,}75=\frac{5\pi}{6} \end{align} Từ điểm cuối $P$ là điểm biên, ta lùi lại một cung $\frac{5\pi}{6}$ sẽ đến điểm $P_0$ có tọa độ 3 cm, như hình vẽ:

Hình 7: Biết điểm cuối là điểm biên và biết cung $\Delta\varphi$ ta có thể biết tọa độ của điểm pha ban đầu $P_0$.

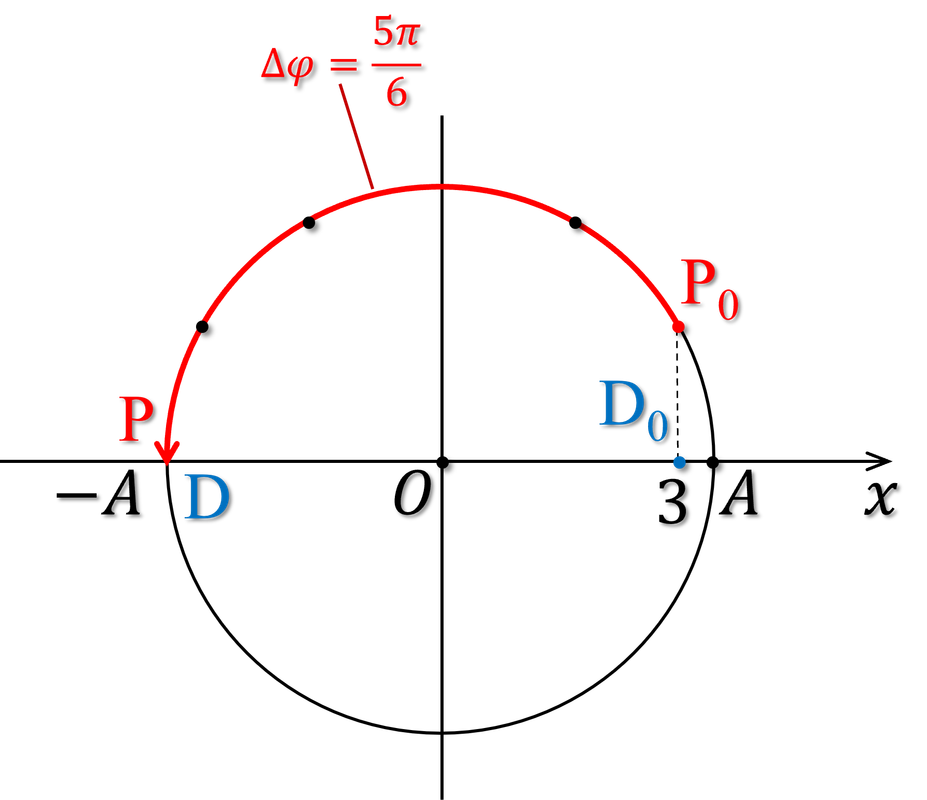
Từ hình vẽ ta thấy \begin{align} 3&=\frac{\sqrt{3}}{2}A\\ &A=2\sqrt{3}\ \text{cm} \varphi=\frac{\pi}{6} \end{align} Tóm lại phương trình chuyển động là \begin{align} x=2\sqrt{3}\cos{\left(\frac{10\pi}{9}t+\frac{\pi}{6}\right)}\ \text{cm} \end{align}

Câu 8 . Tìm biên độ dao động

Đáp án D

Giả sử phương trình dao động là $x=A\cos{\left(\omega t+\varphi\right)}$. Với các giá trị $x$ và $t$ đã cho, ta có hệ phương trình \begin{align} 7&=A\cos{\left(4\pi t_1+\varphi\right)}\tag{8.1}\label{8.1}\\ 24&=A\cos{\left(4\pi \left(t_1+0\text{,}125\right)t+\varphi\right)}\tag{8.2}\label{8.2} \end{align} Đặt $4\pi t_1+\varphi=\alpha$ ta có \begin{align} 7&=A\cos{\left(\alpha\right)}\tag{8.3}\label{8.3}\\ 24&=A\cos{\left(\alpha+\frac{\pi}{2}\right)}\tag{8.4}\label{8.4} \end{align} Chia (\ref{8.4}) cho (\ref{8.3}) vế theo vế ta được \begin{align} \frac{24}{7}=\frac{\cos{\left(\alpha+\frac{\pi}{2}\right)}}{\cos{\left(\alpha\right)}}\tag{8.5}\label{8.5} \end{align} Bấm máy tính Casio giải phương trình (\ref{8.5}) ta được $\alpha=-1\text{,}287$, thay vào (\ref{8.3}) suy ra \begin{align} A=25\ \text{cm} \end{align}

Câu 9 . Tìm biên độ dao động

Đáp án B

Thời gian $\Delta t_1=\frac{T}{6}$ ứng với độ tăng pha $\Delta \varphi_1=\frac{2\pi}{6}$, $\Delta t_2=\frac{T}{3}$ ứng với $\Delta \varphi_2=\frac{2\pi}{3}$. Ban đầu vật ở biên ứng với $P_0$, sau thời gian $\Delta t_1$ vật đến vị trí $\frac{A}{2}$ (ứng với $P_2$), sau thời gian $\Delta t_2$ tiếp theo vật đến biên (ứng với $P_2$), như hình 8 dưới đây:

Hình 8: Quãng đường là hình chiếu của cung pha trên $Ox$.

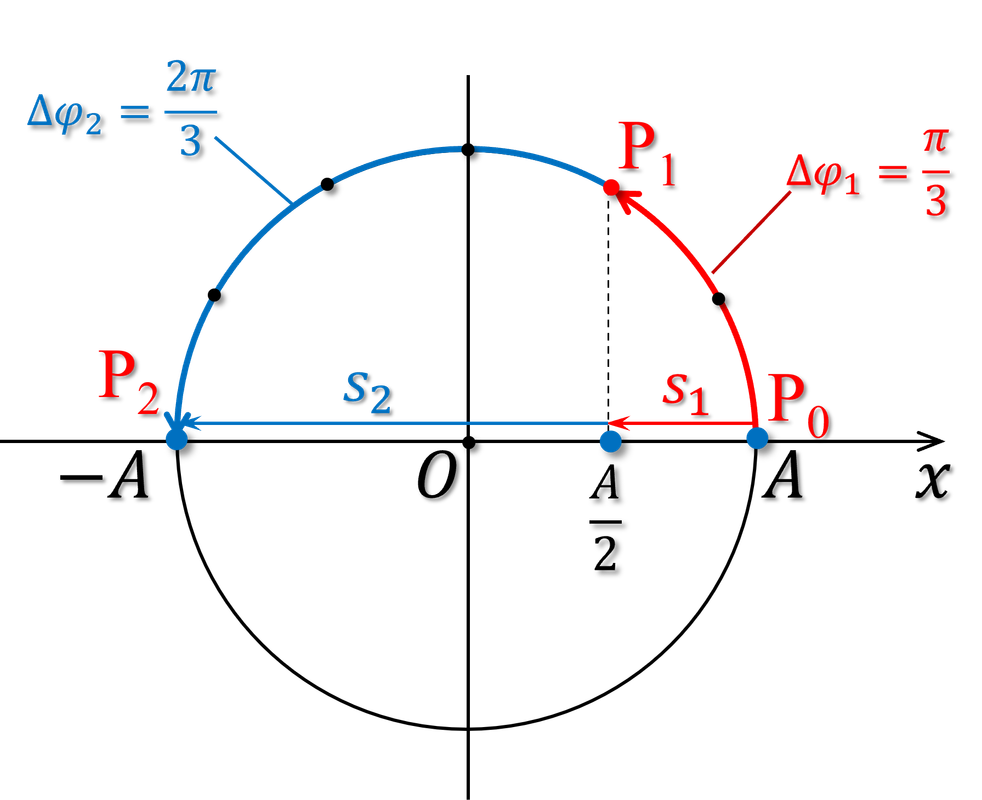
Từ hình vẽ ta thấy \begin{align} s_1&=\frac{A}{2}\\ &s_2=\frac{3A}{2}\\ \end{align} Theo bài ra thì $s_2-s_1=2\ \text{cm}$, tức là \begin{align} \frac{3A}{2}-\frac{A}{2}&=2\ \text{cm}\\ A&=2\ \text{cm} \end{align}

---

---