Hôm nay học sinh cả nước đã bước vào ngày thi thứ hai kì thi TN THPT năm 2023. Để các em học sinh so sánh kết quả làm bài của mình, DẠY HỌC SÁNG TẠO gửi đến các bạn lời giải chi tiết đề thi TN THPT môn Vật lý năm 2023. Đây là lời giải theo chủ quan của tác giả, chỉ mang tính chất tham khảo. Chúc các bạn may mắn.
1 Đề thi TN THPT môn vật lý năm 2023 - Mã đề 209
2 Đáp án 20 câu nhận biết đầu đề thi TN THPT môn vật lý năm 2023 mã đề 209
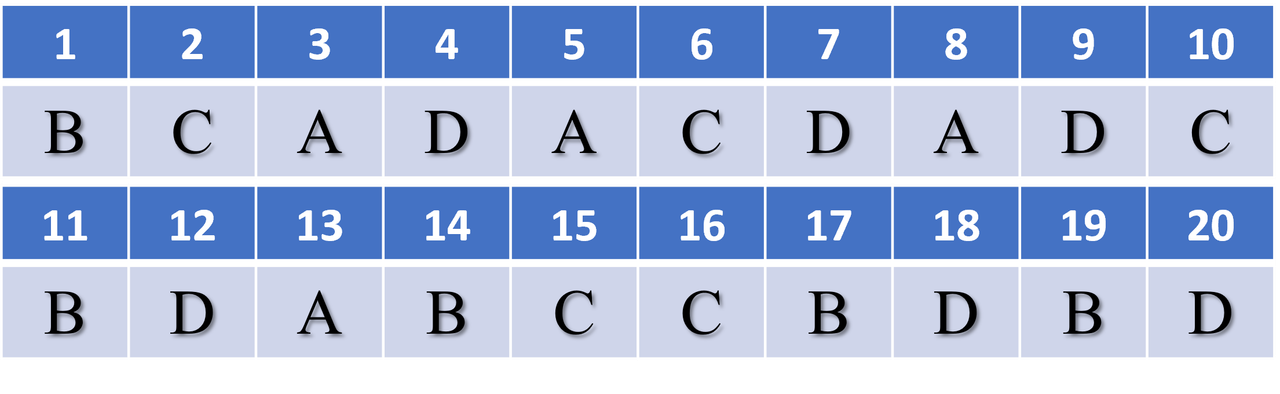 Hình 1: 20 câu đầu đề thi TN THPT môn vật lý năm 2023 ở mức nhận biết và thông hiểu.
Hình 1: 20 câu đầu đề thi TN THPT môn vật lý năm 2023 ở mức nhận biết và thông hiểu.
3 Giải chi tiết đề thi TN THPT môn Vật lý năm 2023 - Mã đề 209
Câu 21 . Giải chi tiết đề vật lý năm 2023 - Mã đề 209
Đáp án A
Biên độ dao động tổng hợp cực đại khi hai dao động thành phần cùng pha, khi đó
Câu 22 . Giải chi tiết đề vật lý năm 2023 - Mã đề 209
Đáp án B
Chú ý đây là câu hỏi yêu cầu chỉ ra phương án sai.
Laze có tính đơn sắc cao, vậy nó là tia đơn sắc, không phải ánh sáng trắng (ánh sáng trắng là tập hợp nhiều ánh sáng đơn sắc).
Câu 23 . Giải chi tiết đề vật lý năm 2023 - Mã đề 209
Đáp án B
Siêu âm là âm có tần số lớn hơn 20.000 Hz.
Câu 24 . Giải chi tiết đề vật lý năm 2023 - Mã đề 209
Đáp án C
Cảm ứng từ tại tâm dòng điện tròn là
Câu 25 . Giải chi tiết đề vật lý năm 2023 - Mã đề 209
Đáp án D
Năng lượng của phôtôn là
Câu 26 . Giải chi tiết đề vật lý năm 2023 - Mã đề 209
Đáp án C
Khoảng vân trong thí nghiệm Y-âng về giao thoa ánh sáng được tính bằng công thức
Câu 27 . Giải chi tiết đề vật lý năm 2023 - Mã đề 209
Đáp án D
Cảm kháng của cuộn cảm trong mạch điện xoay chiều là
Câu 28 . Giải chi tiết đề vật lý năm 2023 - Mã đề 209
Đáp án B
Tần số góc dao động của con lắc đơn là
Câu 29 . Giải chi tiết đề vật lý năm 2023 - Mã đề 209
Đáp án B
Chu kì tính theo tần số riêng của mạch dao động
Câu 30 . Giải chi tiết đề vật lý năm 2023 - Mã đề 209
Đáp án D
Số nuclôn không mang điện là số nơtrôn, nó bằng
Câu 31 . Giải chi tiết đề vật lý năm 2023 - Mã đề 209
Đáp án C
Trước hết ta tính tần số góc
Ta vẽ đường tròn pha
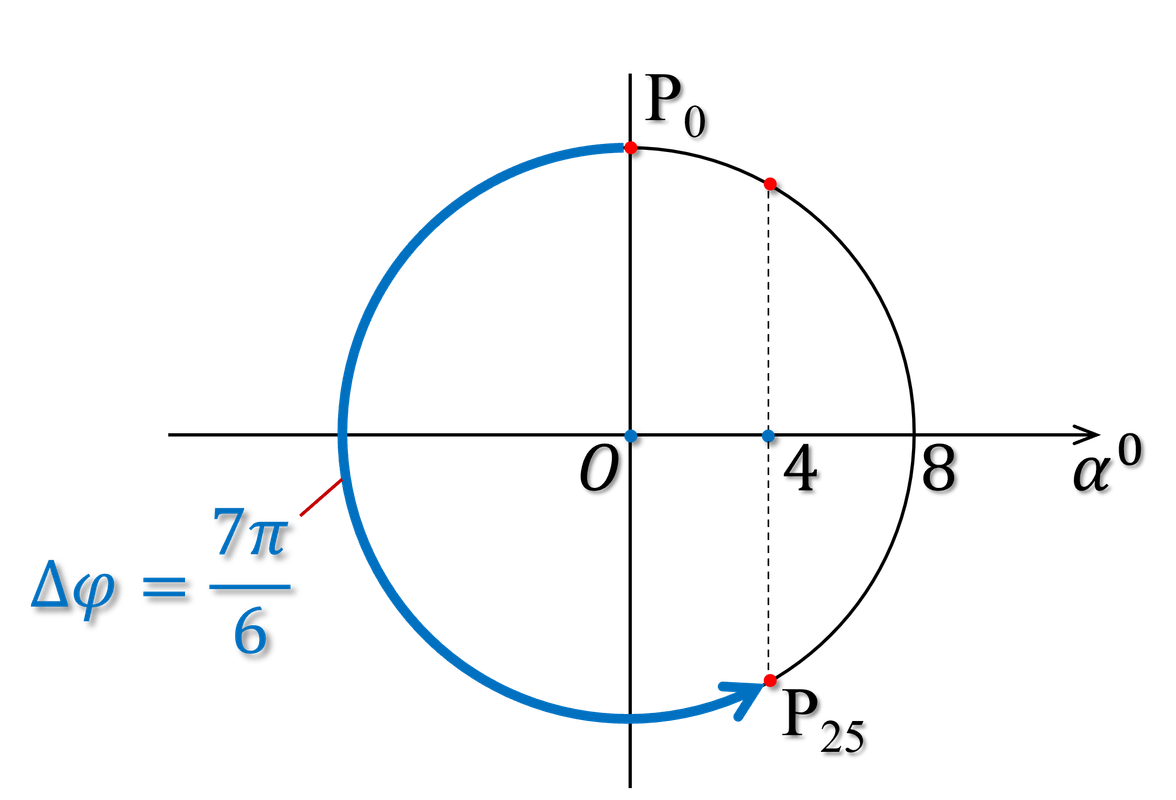 Hình 2: Giải bài toán thời gian trong dao động điều hòa bằng đường tròn pha.
Hình 2: Giải bài toán thời gian trong dao động điều hòa bằng đường tròn pha.
Cứ mỗi chu kì (điểm pha P đi được một vòng) thì vật nhỏ đi qua li độ 2 lần. Sau 12 vòng thì vật nhỏ qua li độ này 24 lần, lúc đó nó ở VTCB theo chiều âm. Vật đi qua li độ này lần thứ 25 tức là nó đi thêm một cung
Thời gian là
Câu 32 . Giải chi tiết đề vật lý năm 2023 - Mã đề 209
Đáp án B
Trong mạch , nếu thay đổi để cực đại thì trong mạch có cộng hưởng điện. Khi đó
cùng pha với cường độ dòng điện, nên chậm pha so với , ta có
Câu 33 . Giải chi tiết đề vật lý năm 2023 - Mã đề 209
Đáp án B
Ta tính cảm kháng và dung kháng
Tổng trở của mạch
Cường độ hiệu dụng
Câu 34 . Giải chi tiết đề vật lý năm 2023 - Mã đề 209
Đáp án B
Độ dài một bó sóng bằng nửa bước sóng, tức là bằng 18 cm. Trong khi đó , chứng tỏ M thuộc bó thứ hai kể từ A. N cùng biên độ với M và xa M nhất (N gần B nhất) tức là giữa N và B không có nút sóng nào. Tóm lại, ngoài 2 nút A và B, giữa MN còn 5 nút, giữa AM còn 1 nút, tất cả là 8 nút. Tương ứng với 7 bó. Chiều dài sợi dây là
Câu 35 . Giải chi tiết đề vật lý năm 2023 - Mã đề 209
Đáp án D
Tần số góc của mạch và điện tích cực đại
Phương trình điện tích tức thời và suy ra phương trình cường độ dòng điện tức thời trong mạch dao động
Thay và vào ta được phương trình
Câu 36 . Giải chi tiết đề vật lý năm 2023 - Mã đề 209
Đáp án C
Ở đồ thị, chu kì tức là .
Điện áp hiệu dụng hai đầu mạch luôn lớn hơn hai đầu , nên hai đồ thị biên độ bằng nhau chắc chắn không thể là đồ thị của . Tức là đồ thị có biên độ lớn là đồ thị của . Từ đồ thị ta thấy
chậm pha hơn một lượng , chậm pha hơn một lượng cũng bằng . Ta vẽ giản đồ véc tơ.
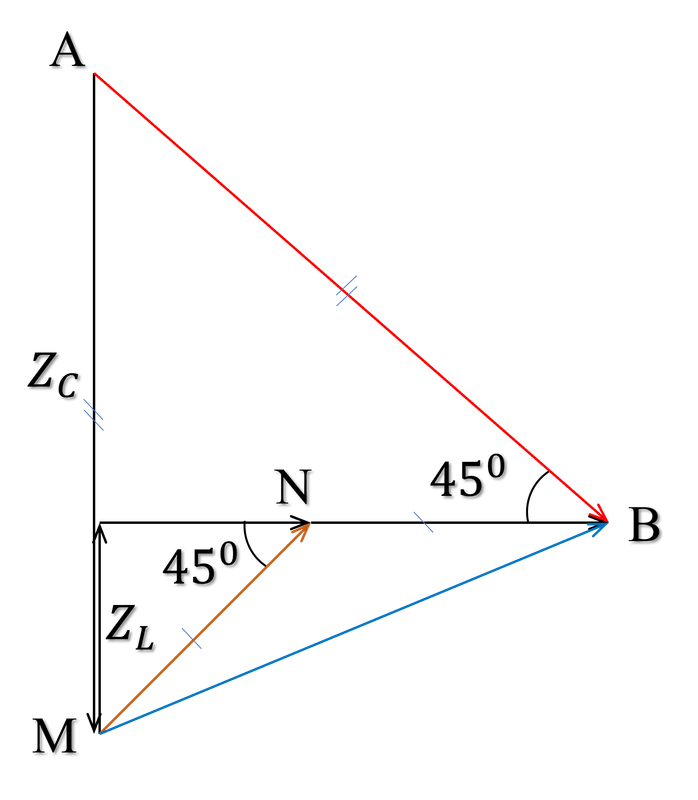 Hình 3: Giản đồ véc tơ câu 36 đề thi TN THPT môn Vật lý năm 2023.
Hình 3: Giản đồ véc tơ câu 36 đề thi TN THPT môn Vật lý năm 2023.
Trong giản đồ, ta có
Khi cộng hưởng ta có
Chia () cho () vế theo vế, biến đổi một chút ta rút ra được
Câu 37 . Giải chi tiết đề vật lý năm 2023 - Mã đề 209
Đáp án D
Gọi số hạt X và số hạt Y ở các thời điểm , , lần lượt tương ứng là và , và , và . Theo bài ra thì
Thay () vào (), biến đổi và suy ra được
Mặt khác ta có
Thay () vào (), biến đổi và suy ra được
Kết hợp () và () (để dễ giải ta đặt và ) ta suy ra
Câu 38 . Giải chi tiết đề vật lý năm 2023 - Mã đề 209
Đáp án B
Câu thí nghiệm Y-âng về giao thoa ánh sáng này chúng ta sử dụng máy tính Casio để giải. Các bạn có thể tham khảo phương pháp này tại đây: GIẢI BÀI TẬP GIAO THOA ÁNH SÁNG BẰNG MÁY TÍNH CASIO
Tại M có vân sáng của bức xạ bậc trùng với vân sáng của bức xạ bậc , tức là
Dùng chức năng table của máy tính Casio, lần lượt cố định và cho chạy từ đến . Kết quả ta tìm thấy
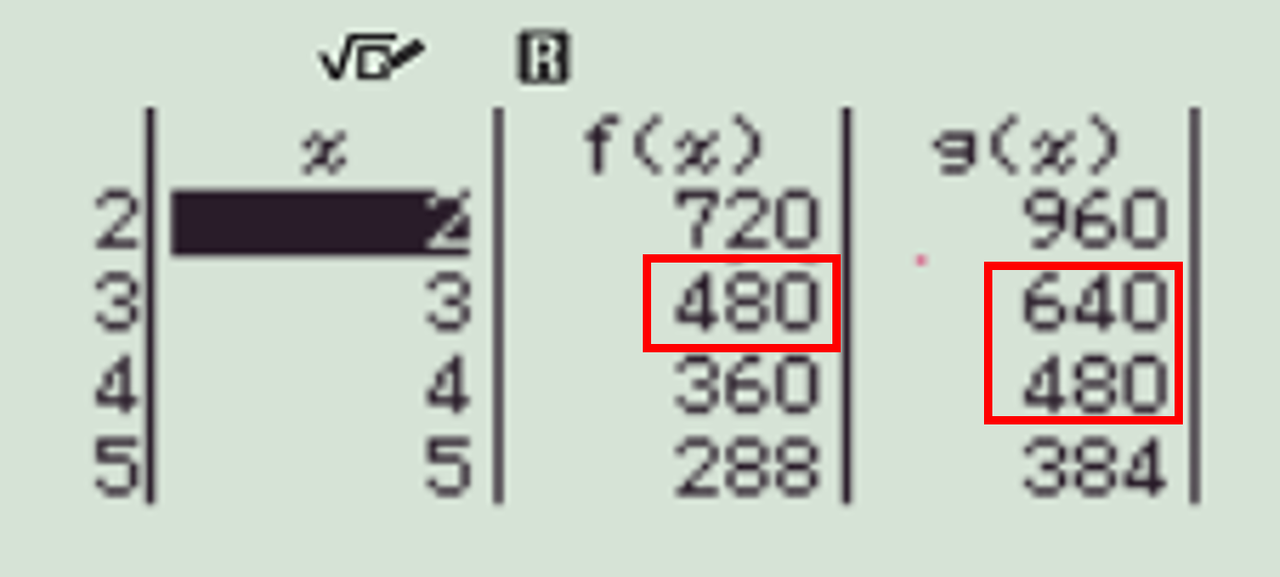 Hình 4: Sử dụng bảng trong máy Casio giải câu 38 đề thi TN THPT môn Vật lý năm 2023.
Hình 4: Sử dụng bảng trong máy Casio giải câu 38 đề thi TN THPT môn Vật lý năm 2023.
Ở cột tôi đã đặt và thấy rằng chỉ có 2 bước sóng nằm trong khoảng từ 390 nm đến 710 nm cho vân sáng tại M, đó là vân sáng bậc của bức xạ (đã cho) và vân sáng bậc của bức xạ .
Bây giờ ta giả sử tại N có vân sáng bậc của bức xạ , khi đó
Tiếp tục dùng table của máy tính Casio, cho chạy từ đến , ta được
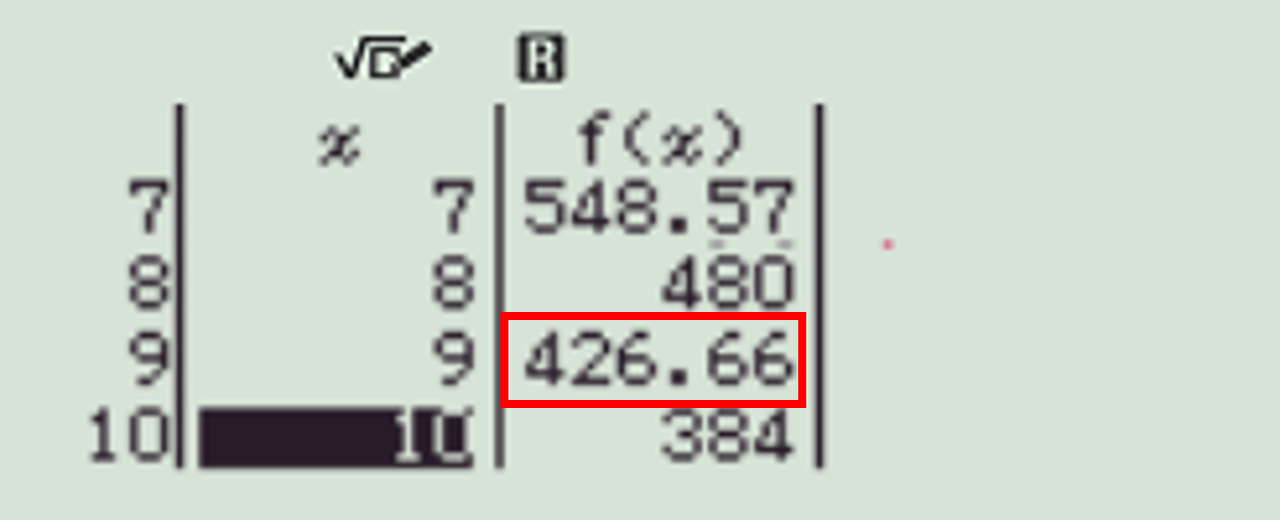 Hình 5: Tiếp tục sử dụng bảng trong máy Casio giải câu 38 đề thi TN THPT môn Vật lý năm 2023.
Hình 5: Tiếp tục sử dụng bảng trong máy Casio giải câu 38 đề thi TN THPT môn Vật lý năm 2023.
Bước sóng nhỏ nhất cho vân sáng tại N là
Câu 39 . Giải chi tiết đề vật lý năm 2023 - Mã đề 209
Đáp án C
Xét sự dao động điều hòa của M trong hai giai đoạn:
+ Giai đoạn thứ nhất: Từ khi M được thả nhẹ đến khi N rời khỏi nó.
Trong thời gian này vật M dao động với lực đàn hồi và trọng lực biểu kiến (hợp lực của trọng lực với lực ma sát trượt do N tác dụng - Chú ý lực ma sát trượt do N tác dụng lên M có hướng thẳng đứng hướng xuống) . Vị trí cân bằng của M trong thời gian này là vị trí lò xo dãn một đoạn bằng
Vì M được thả nhẹ từ vị trí lò xo không biến dạng nên vị trí thả là biên, biên độ là .
Tần số góc trong thời gian này là
Thời gian ứng với độ tăng pha . Vật bắt đầu từ biên nên sau thời gian này nó đến li độ có độ lớn (tại đây lò xo dãn 9 cm).
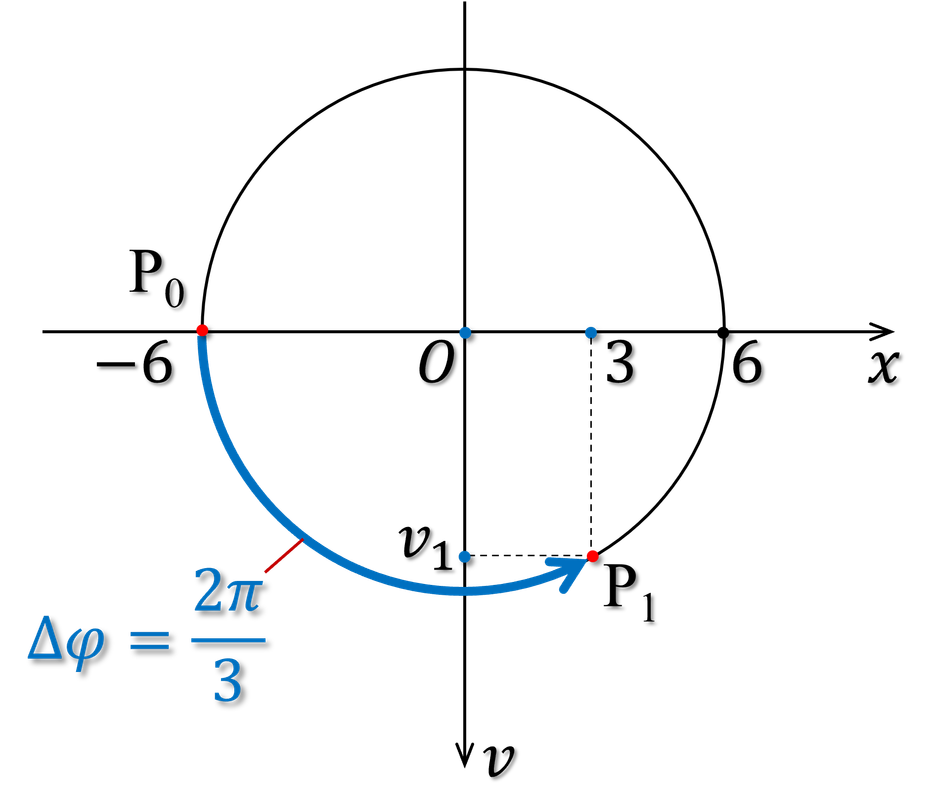 Hình 6: Dùng đường tròn pha giải câu 39 đề thi TN THPT môn Vật lý năm 2023.
Hình 6: Dùng đường tròn pha giải câu 39 đề thi TN THPT môn Vật lý năm 2023.
Tại đây vận tốc của M có độ lớn
+ Giai đoạn thứ hai: N đã rời khỏi M, vật M dao động điều hòa với trọng lực và lực đàn hồi. Vị trí cân bằng bây giờ là vị trí lò xo dãn , nên vị trí của M khi N rời khỏi nó có li độ , tần số góc , biên độ mới là
Độ dãn cực đại của lò xo
Chú ý: Ta có thể giải nhanh hơn rất nhiều bằng định luật bảo toàn có năng cho giai đoạn thứ hai. Các bạn tham khảo tại đây (Câu 39): GIẢI CHI TIẾT ĐỀ THAM KHẢO TN THPT 2023 MÔN VẬT LÝ.
Câu 40 . Giải chi tiết đề vật lý năm 2023 - Mã đề 209
Đáp án C
Nếu A và B là các nguồn sóng, C là cực tiều thứ 4, tức là
Nếu B và C là các nguồn thì A là cực tiểu thứ , khi đó
Từ () và () suy ra
Do nên suy ra
Số cực tiểu trên BC đạt cực đại khi cực đại, tức là . Khi đó kết hợp () và (), chú ý thêm rằng , ta viết được
Chia cả hai vế cho , đặt , ta giải tìm được
Các cực tiểu trên BC bây giờ là , có tất cả 14 cực tiểu.











Tại sao \left(AC\right)^2=\left(\lambda+BC\right)^2 vậy ạ?
Trả lờiXóaBạn suy luận rằng từ phương trình
XóaXuống phương trình
Là vì
Nhưng không phải như vậy. Bạn phải biến đổi và kết hợp với (40.1), (40.3) và