Đề thi vào lớp 10 chuyên lý thành phố Hải Phòng năm 2023 có lời giải chi tiết
Ngày 5 và 6/6/2023 thành phố Hải Phòng bắt đầu kì thi tuyển sinh vào lớp 10 chuyên. Trong những ngày này, các em học sinh vừa tham gia kì thi và phụ huynh rất nóng lòng về kết quả. Để giúp học sinh và phụ huynh có thêm một chút thông tin, DẠY HỌC SÁNG TẠO xin chia sẻ Đề thi vào lớp 10 chuyên lý thành phố Hải Phòng năm 2023 có lời giải chi tiết. Đây không phải là đáp án chính thức nên không có thang điểm chi tiết, nhưng các em có thể so sánh với bài làm của mình để nhận định tương đối điểm số mình đạt được.
1 Đề và đáp án thi vào lớp 10 chuyên lý Hải Phòng 2023
Câu 1 (2,0 điểm). Đề và đáp án thi vào lớp 10 chuyên lý Hải Phòng 2023
Trên đoạn đường thẳng có hai địa điểm M và N cách nhau $240\ \text{m}$. Tại thời điểm $t = 0$, An và Bình chạy cùng chiều từ N với tốc độ không đổi lần lượt là $v_1 = 2\ \text{m/s}$, $v_2 = 4\ \text{m/s}$, đồng thời Cường đạp xe từ M với tốc độ không đổi $v_3 = 10\ \text{m/s}$ đuổi theo An và Bình dọc theo đường thẳng như hình 1.
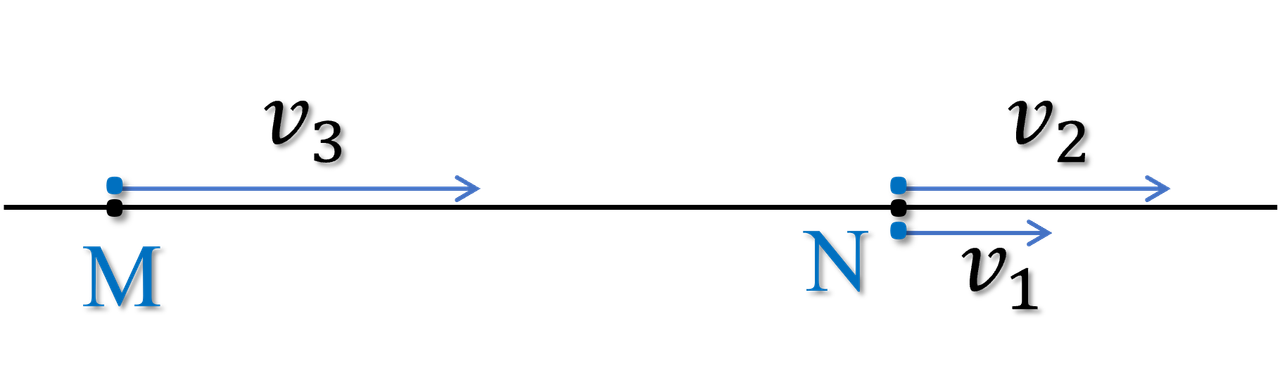
- Cường đuổi kịp Bình tại vị trí P. Tìm khoảng cách MP.
- Trước khi Cường đuổi kịp Bình thì thời điểm nào một người cách đều hai người còn lại?
- Tại thời điểm $t = 0$, Đức xuất phát tại M chạy với tốc độ không đổi $v_4$ đuổi theo An va Bình. Khoảng thời gian từ khi Đức gặp An đến khi Đức gặp Bình là $20\ \text{s}$. Tính $v_4$.
1. Xác định vị trí P tại đó Cường đuổi kịp Bình
Thờ gian Cường đi từ M đến P bằng thời gian Bình đi từ N đến P, nó được tính bằng hai vế của phương trình sau:
\begin{align}
\frac{MP}{v_3}&=\frac{MP-240}{v_2}\\
MP&=\frac{240v_3}{v_3-v_2}\\
&=\frac{240\times10}{10-4}\\
&=400\ \text{m}
\end{align}
2. Thời điểm $t_1$ có một người cách đều hai người còn lại
Trường hợp 1: An cách đều Cường và Bình.
\begin{align}
240+v_1t_1&=\frac{1}{2}\left[v_3t_1+\left(240+v_2t_1\right)\right]\\
t_1&=\frac{240}{v_3+v_2-2v_1}\\
&=\frac{240}{10+4-2\times 2}=24\ \text{s}
\end{align}
Trường hợp 2: Cường cách đều An và Bình.
\begin{align}
v_3t_1&=\frac{1}{2}\left[\left(240+v_1t_1\right)+\left(240+v_2t_1\right)\right]\\
t_1&=\frac{480}{2v_3-v_2-v_1}\\
&=\frac{480}{2\times10-4-2}\approx34\text{,}3\ \text{s}
\end{align}
3. Thời điểm $t_1$ có một người cách đều hai người còn lại
Thời gian từ $t=0$ đến khi Đức đuổi kịp An là
$$
t_\text{ĐA}=\frac{240}{v_4-v_1}=\frac{240}{v_4-2}
$$
Thời gian từ $t=0$ đến khi Đức đuổi kịp Bình là
$$
t_\text{ĐB}=\frac{240}{v_4-v_2}=\frac{240}{v_4-4}
$$
Theo bài ra thì giữa hai thời điểm này là 20 s, tức là ta có
\begin{align}
\frac{240}{v_4-4}-\frac{240}{v_4-2}=20
\end{align}
Suy ra nghiệm dương
$$
v_4=8\ \text{m/s}
$$
Câu 2 (2,0 điểm). Đề và đáp án thi vào lớp 10 chuyên Lý Hải Phòng 2023
Một nhiệt lượng kế cách nhiệt chứa hỗn hợp gồm nước đá có khối lượng $m$ và một chất rắn $X$ dễ nóng chảy cỏ khối lượng $m_1 = 1\text{,}05m$. Người ta nhúng sợi đốt có công suất không đổi $P$ để cấp nhiệt cho hỗn hợp trên. Nhiệt độ ban đầu của hỗn hợp là $-40\ \text{°C}$. Dùng một nhiệt kế nhúng vào nhiệt lượng kế và theo dõi sự phụ thuộc nhiệt độ của hỗn hợp theo thời gian $T$ trong khoảng thời gian từ 0 đến 50 phút thì thu được đồ thị như hình 2. Biết nhiệt dung riêng của nước đá là $c = 2100\ \text{J/kg.K}$; nhiệt dung riêng cùa chất $X$ ở trạng thái rắn là $c_1 = 1200\ \text{J/kg.K}$. Coi chỉ có sự trao đổi nhiệt giữa sợi đốt, chất rắn $X$ và nước đá. Hãy xác định:
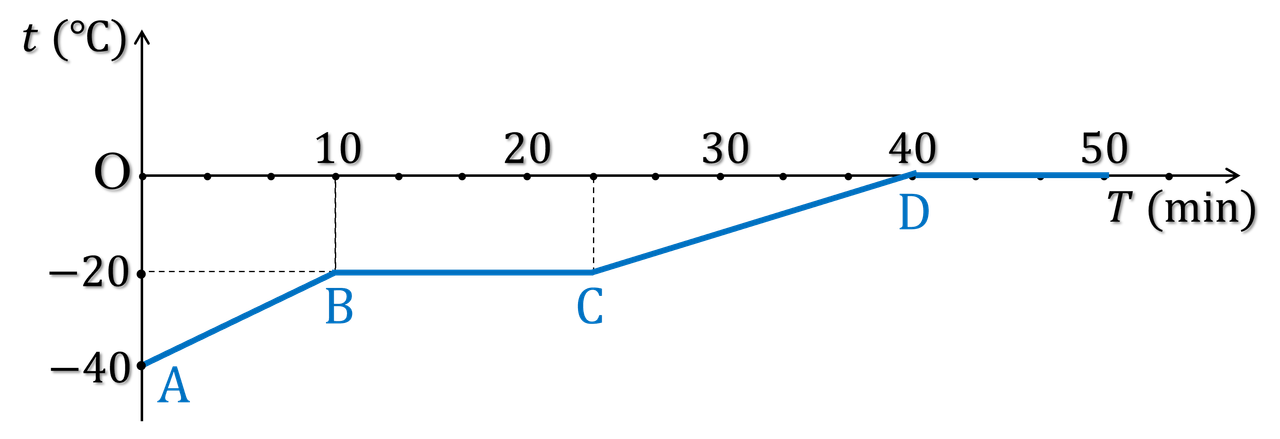
- Nhiệt nóng chảy $\lambda$ của chất rắn $X$.
- Nhiệt dung riêng $c_2$ của chất rắn $X$ ở trạng thái lỏng.
1. Nhiệt nóng chảy $\lambda$ của chất rắn $X$
Nhiệt độ nóng chảy của nước đá là $0\ \text{°C}$, vậy nên trong khoảng thời gian từ 0 đến 40 phút nước đá chưa tan. Đoạn thẳng nằm ngang của đồ thị (từ 10 đến $\frac{70}{3}$ phút) biểu diễn quá trình nóng chảy của chất $X$. Nhiệt lượng trong khoảng thời gian này có thể tính theo công suất $P$ (vế trái) và tính theo nhiệt nóng chảy $\lambda$ (vế phải), như sau:
\begin{align}
P\Delta T&=1\text{,}05m\lambda\\
\Rightarrow \lambda&=\frac{P\Delta T}{1\text{,}05m}\tag{2.1}\label{2.1}
\end{align}
Trong đó $\Delta T=20-10=10\ \text{min}$, công suất $P$ và khối lượng $m$ được xác định bằng đoạn đồ thị đầu tiên (từ 0 đến 10 phút):
\begin{align}
P\Delta T_1&=\left(1\text{,}05mc_1+mc\right)\Delta t_1\\
\frac{P}{m}&=\frac{\left(1\text{,}05c_1+c\right)\Delta t_1}{\Delta T_1}\tag{2.2}\label{2.2}
\end{align}
Thay (\ref{2.2}) vào (\ref{2.1}), ta được
\begin{align}
\lambda&=\frac{\left(1\text{,}05c_1+c\right)\Delta t_1}{\Delta T_1}\times \frac{\Delta T}{1\text{,}05}\\
&=\frac{\left(1\text{,}05.1200+2100\right).20}{10}\times \frac{\frac{40}{3}}{1\text{,}05}\\
&\approx 8\text{,}53.10^4\ \text{J/kg}
\end{align}
2. Nhiệt dung riêng $c_2$ của chất $X$ lỏng
Ở đoạn đồ thị CD, ta có phương trình
\begin{align}
P\frac{50}{3}&=\left(1\text{,}05mc_2+mc\right)\times 20\\
c_2&=\frac{1}{1\text{,}05}\left(\frac{5P}{6m}-c\right)
\end{align}
Kết hợp với (\ref{2.2}), ta tính được
$$
c_2=3\text{,}33.10^3\ \text{J/kg.K}
$$
Câu 3 (3,0 điểm). Đề và đáp án thi vào lớp 10 chuyên lý Hải Phòng 2023
Một đoạn mạch AB gồm nguồn điện có điện áp $U$ nối với điện trở $r = 8\ \Omega$ như hình 3. Bỏ qua điện trờ của dây nối và điện trở chỗ tiếp xúc trong tất cả các trường hợp.
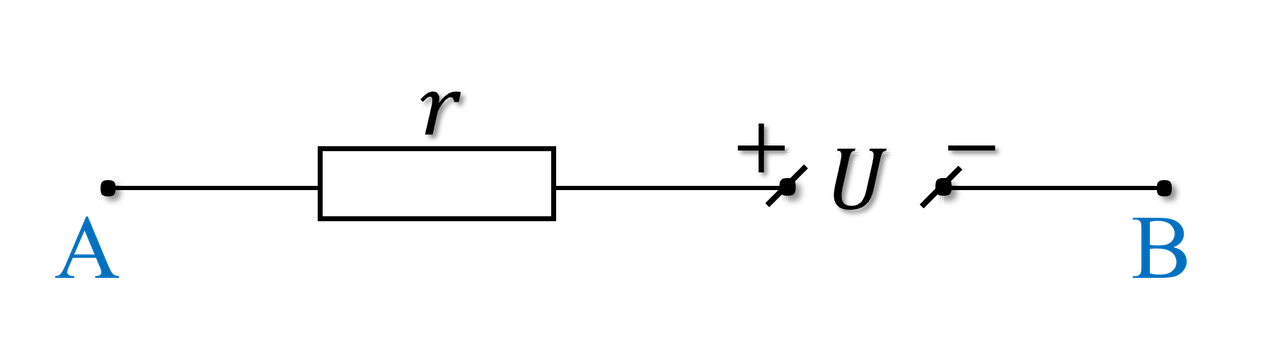
- Mắc vào hai đầu A, B một bóng đèn ghi $8\ \text{V} - 4\ \text{W}$. Giá trị điện áp $U$ thoả mãn điều kiện nào để dòng điện chạy qua đèn đạt từ $95\ \text{%}$ đến $105\ \text{%}$ cường độ dòng điện định mức của đèn? Coi điện trở của bóng đèn không đổi và đèn không bị “cháy”.
- Đặt điện áp $U = 20\ \text{V}$ luôn không đổi:
- Tháo bỏ bóng đèn khỏi 2 đầu A, B. Mắc vào A, B bộ 4 điện trở giống nhau có cùng giá trị $R = 6\ \Omega$. Hãy xác định cách ghép 4 điện trở $R$ để công suất trên bộ 4 điện trở này đạt giá trị lớn nhất; nhỏ nhất.
- Tháo bỏ 4 điện trở $R$ khỏi 2 đầu A, B. Cho $n$ điểm theo thứ tự $A_1$, $A_2$, ..., $A_n$ ($A_n\gt 8$) các đỉnh của một đa giác đều. Giữa hai điểm liên tiếp mắc một điện trở $R_0 = 4\ \Omega$, tạo thành vòng điện trở khép kín. Mắc hai đầu A, B vào cặp đỉnh $A_1$, $A_3$ hoặc cặp đỉnh $A_1$, $A_6$ thì tổng công suất tiêu thụ trên vòng điện trở như nhau. Tính $n$.
- Tháo bỏ vòng điện trở khỏi hai đầu A, B. Mắc vào A, B động cơ điện một chiều có điện trở tổng cộng là $R’ = 12\ \Omega$. Động cơ kéo một vật có trọng lượng $P = 50\ \text{N}$ chuyền động thẳng đều theo phương thẳng đứng với tốc độ $v$. Bỏ qua mọi ma sát và lực cản. Tìm tốc độ lớn nhất của vật.
1. Mắc giữa A và B một bóng đèn
Điện trở và cường độ định mức của các đèn lần lượt là
\begin{align}
R_\text{Đ}&=\frac{U_\text{đ}^2}{P_\text{đ}}\\
&=\frac{8^2}{4}=16\ \Omega\\
\end{align}
Cường độ dòng điện qua đèn và công suất tiêu thụ của đèn
\begin{align}
I&=\frac{U}{R_\text{Đ}+r}\\
P&=I^2R_\text{Đ}\\
&=\frac{U^2R_\text{Đ}}{\left(R_\text{Đ}+r\right)^2}\tag{3.1}\label{3.1}\\
&=\frac{U^2}{36}
\end{align}
Mức độ sáng của đèn tỉ lệ với công suất tiêu thụ, theo yêu cầu của bài toán thì
\begin{align}
\frac{95}{100}P_\text{đ}\ge P \ge \frac{105}{100}P_\text{đ}\\
\frac{95}{100}\times4\ge \frac{U^2}{36} \ge \frac{105}{100}\times4\\
11\text{,}7\ \text{V}\le U \le 12\text{,}3\ \text{V}
\end{align}
2a. Mắc giữa A và B bộ 4 điện trở giống nhau
Ta tính công suất trên bộ điện trở $R_\text{b}$ bằng công thức (\ref{3.1}), tức là
\begin{align}
P=\frac{U^2R_\text{b}}{\left(R_\text{b}+r\right)^2}\tag{3.2}\label{3.2}
\end{align}
Chia cả tử cả mẫu cho $R_\text{b}$ ta được
\begin{align}
P=\frac{U^2}{\left(\sqrt{R_\text{b}}+\frac{r}{\sqrt{R_\text{b}}}\right)^2}
\end{align}
Áp dụng bất đẳng thức Côssi:
\begin{align}
\sqrt{R_\text{b}}+\frac{r}{\sqrt{R_\text{b}}}&\ge 2\sqrt{\sqrt{R_\text{b}}.\frac{r}{\sqrt{R_\text{b}}}}=2\sqrt{r}\\
\Rightarrow P&\le \frac{U^2}{4r}
\end{align}
Như vậy $P=P_\text{max}=\frac{U^2}{4r}$ khi $R_\text{b}=r=8\ \Omega$.
Để có được điện trở tương đương của bộ 4 điện trở $R=6\ \Omega$ bằng $8\ \Omega$, ta ghép 3 điện trở song song nhau và nối tiếp với điện trở còn lại, khi đó
$$
R_\text{b}=R+\frac{R}{3}=8\ \Omega
$$
Điện trở của bộ lớn nhất khi 4 điện trở mắc nối tiếp với nhau: $R_\text{max}=4R=24\ \Omega$, khi đó công suất là
\begin{align}
P&=\frac{24U^2}{\left(24+8\right)^2}\\
&\approx0\text{,}0234U^2
\end{align}
Điện trở của bộ nhỏ nhất khi 4 điện trở mắc song song với nhau: $R_\text{max}=\frac{R}{4}=1\text{,}5\ \Omega$, khi đó công suất là
\begin{align}
P&=\frac{1\text{,}5U^2}{\left(1\text{,}5+8\right)^2}\\
&\approx0\text{,}0166U^2
\end{align}
Vậy công suất lớn nhất khi ghép 3 điện trở song song rồi nối tiếp với điện trở còn lại; công suất nhỏ nhất khi ghép 4 điện trở song song với nhau.
2b. Mắc giữa A và B một vòng điện trở hình đa giác $n$ đỉnh
Khi mắc $A$ và $B$ vào $A_1$ và $A_3$ ta được điện trở mạch $AB$ là
\begin{align}
R_1=\frac{2R\left(n-3\right)R}{\left(n-1\right)R}=\frac{2\left(n-3\right)R}{n-1}
\end{align}
Khi mắc $A$ và $B$ vào $A_1$ và $A_6$ ta được điện trở mạch $AB$ là
\begin{align}
R_2=\frac{5R\left(n-6\right)R}{\left(n-1\right)R}=\frac{5\left(n-6\right)R}{n-1}
\end{align}
Từ biểu thức tính công suất trên bộ điện trở (\ref{3.2}), ta suy ra dạng phương trình bậc 2
\begin{align}
R_\text{b}^2-\left(\frac{U^2}{P}-2r\right)R_\text{b}+r^2=0\tag{3.3}\label{3.3}
\end{align}
Với $R_\text{b}=R_1$ hoặc $R_\text{b}=R_2$ thì công suất bằng nhau và bằng $P_12$, tức là $R_\text{b}=R_1$ và $R_\text{b}=R_2$ là hai nghiệm của phương trình
\begin{align}
R_\text{b}^2-\left(\frac{U^2}{P_12}-2r\right)R_\text{b}+r^2=0\tag{3.4}\label{3.4}
\end{align}
Áp dụng định lí Viet ta có
\begin{align}
R_1R_2&=r^2\\
\frac{2\left(n-3\right)R}{n-1}.\frac{5\left(n-6\right)R}{n-1}&=r^2
\end{align}
Với $R=R_0=4\ \Omega$ và $r=8\ \Omega$, ta tìm được
$$
n=11
$$
2c. Mắc giữa A và B một động cơ điện một chiều
Lực kéo của động cơ bằng trọng lượng của vật $F=50\ \text{N}$, công của lực bằng công của động cơ khi kéo vật lên một quãng đường $s=vt$ là $A=Fs=Fvt$, suy ra công suất có ích của động cơ là $P_i=\frac{A}{t}=Fv$.
Gọi $P_\text{tp}$ là công suất toàn phần do nguồn cung cấp cho mạch, công suất hao phí trên cả động cơ và điện trở $r$ là
\begin{align}
P_\text{hp}=\frac{P_\text{tp}^2\left(R''+r\right)}{U^2}
\end{align}
Công suất toàn phần $P_\text{tp}$ bằng tổng công suất hao phí và công suất có ích
\begin{align}
P_\text{tp}=Fv+\frac{P_\text{tp}^2\left(R''+r\right)}{U^2}
\end{align}
Thay số $R''=12\ \Omega$, $U=20\ \text{V}$, $r=8\ \Omega$, đặt $x=P_\text{tp}$, ta được
\begin{align}
v&=10^{-3}\left[100-\left(x-10\right)^2\right]\\
\Rightarrow v&\le 10^{-1}\ \text{m/s}
\end{align}
Vậy tốc độ cực đại $v_\text{max}=10\ \text{cm/s}$, tốc độ này đạt được khi công suất toàn phần $P_\text{tp}=10\ \text{W}$. Công suất này nhỏ hơn công suất cực đại tính được ở trên nên chấp nhận được.
Câu 4 (2,0 điểm). Đề và đáp án thi vào lớp 10 chuyên lý Hải Phòng 2023
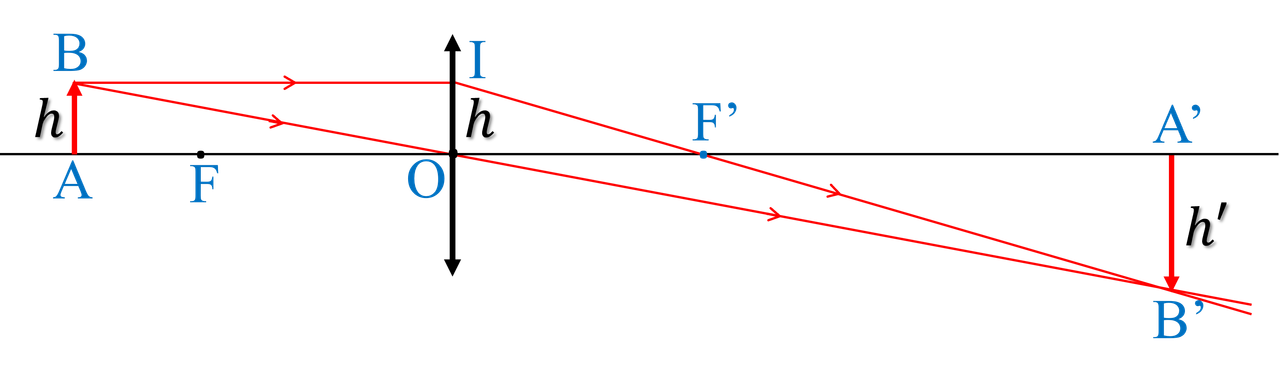
Cho thấu kính hội tụ có quang tâm $O$, tiêu cự $f$ xác định và vật nhỏ AB có dạng một đoạn thẳng đặt vuông góc với trục chính, điểm A nằm trên trục chính. A’B’ trên hình 4 là ảnh thật của AB qua thấu kính. Đặt $AF = a$; $A F’ = b$.
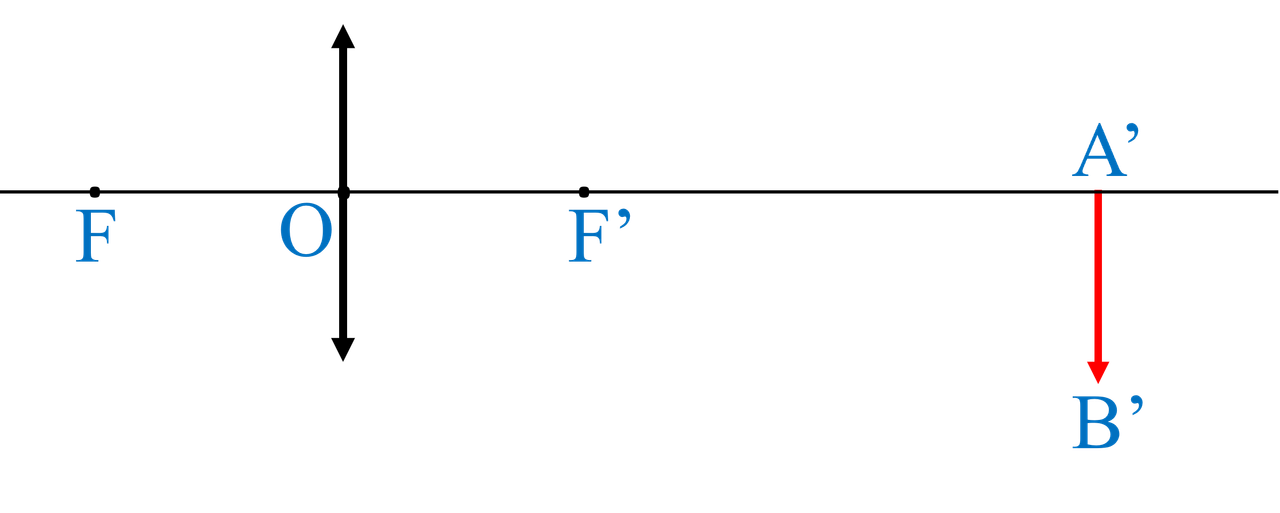
- Dựng hình xác định vị trí của vật AB.
- Chứng minh rằng tích $ab$ không phụ thuộc vào khoảng cách từ vật đến thấu kính.
- Cố định thấu kính, tại thời điểm $t = 0$, cho vật AB dịch chuyển với tốc độ không đổi $v = 2\ \text{cm/s}$ ra xa thấu kính sao cho AB luôn vuông góc với trục chính và A luôn thuộc trục chính. Biết rằng:
- Tại thời điểm $t_1 = 3\ \text{s}$, ảnh của AB là $A_1B_1$ với $A’A_1 = 15\ \text{cm}$.
- Tại thời điểm $t_2 = 11\ \text{s}$, ảnh của AB là $A_2B_2$ với $A’A_2 = 27\text{,}5\ \text{cm}$.
- Tìm $f$.
- Gọi $t_3$ là thời điểm khoảng cách giữa vật và ảnh nhỏ nhất. Từ thời điểm $t_1$ đến thời điểm $t_3$, ảnh của điểm A có tốc độ trung bình bằng bao nhiêu?
Chú ý: Thí sinh có thể sử dụng hoặc không sử dụng công thức thấu kính: $\frac{1}{f}=\frac{1}{d}+\frac{1}{d'}$ và công thức tỉ số chiểu cao của ảnh so với chiều cao của vật: $\frac{h'}{h}=|\frac{d'}{d}|$.
1. Dựng hình xác định vị trí của vật AB
+ Vẽ đường thẳng OB'.
+ Vẽ đoạn thẳng từ B' đi qua F' đến thấu kính tại I.
+ Vẽ đoạn thẳng từ I song song với trục chính, cắt đường thẳng OB' tại B.
+ Vẽ đoạn thẳng từ B vuông góc với trục chính tại A.
2. Chứng minh tích $ab$ không phụ thuộc vào $d$
Từ hình vẽ và kết hợp với công thức thấu kính, ta có
\begin{align}
ab&=\left(d-f\right)\left(d'-f\right)\\
&=\left(d-f\right)\left(\frac{df}{d-f}-f\right)\\
&=f^2\tag{4.1}\label{4.1}
\end{align}
Kết quả cho thấy $ab$ không phụ thuộc $d$.
3a. Tính tiêu cự $f$
Điều đầu tiên cần khẳng định là vật và ảnh luôn chuyển động cùng chiều, tức là nếu vật ra xa thấu kính thì ảnh lại gần thấu kính. Hay nếu $d+s$ thì $d'-s'$.
+ Tại thời điểm $t_1=3\ \text{s}$, vật dời xa vị trí ban đầu một khoảng $s_1=vt_1=6\ \text{cm}$, trong khi đó ảnh dời $s_1'=15\ \text{cm}$ so với vị trí ban đầu của nó (bài toán cho).
+ Tại thời điểm $t_2=11\ \text{s}$, vật dời xa vị trí ban đầu một khoảng $s_2=vt_2=22\ \text{cm}$, trong khi đó ảnh dời $s_2'=27\text{,}5\ \text{cm}$ so với vị trí ban đầu của nó (bài toán cho).
Áp dụng (\ref{4.1}) ta được hệ phương trình
\begin{cases}
ab=f^2\\
\left(a+6\right)\left(b-15\right)=f^2\\
\left(a+22\right)\left(b-27\text{,}5\right)=f^2
\end{cases}
Biến đổi và rút gọn, ta được hệ phương trình bậc nhất hai ẩn:
\begin{cases}
15a-6b=-90\\
27\text{,}5a-22b=-605
\end{cases}
Giải hệ phương trình ta được $a=10\ \text{cm}$ và $b=40\ \text{cm}$, suy ra
$$
f=\sqrt{ab}=20\ \text{cm}
$$
3b. Khoảng cách nhỏ nhất giữa vật và ảnh
\begin{align}
\ell&=d+d'\\
&=d+\frac{20d}{d-20}\\
&=d-20+\frac{400}{d-20}+40
\end{align}
Áp dụng bất đẳng thức Côsi ta được
\begin{align}
\ell&\ge 2\sqrt{\left(d-20\right)\left(\frac{400}{d-20}\right)}+40\\
\ell_\text{min}&\ge80\ \text{cm}
\end{align}
Cực tiểu này đạt được khi
\begin{align}
d-20&=\frac{400}{d-20}\\
d&=40\ \text{cm}\\
d'&=40\ \text{cm}
\end{align}
Tại thời điểm $t_1$ ảnh và vật cách thấu kính các khoảng lần lượt
\begin{align}
d_1'&=f+b-15\\
&=20+40-15=45\ \text{cm}\\
d_1&=f+a+6\\
&=20+10+6=36\ \text{cm}
\end{align}
Đến thời điểm $t_3$ ảnh và vật đã di chuyển được các quãng đường lần lượt là
\begin{align}
s'&=45-40=5\ \text{cm}\\
s&=40-36=4\ \text{cm}
\end{align}
Tốc độ trung bình của vật và ảnh trong thời gian này liên hệ với nhau
\begin{align}
\frac{s}{v}&=\frac{s'}{v'}\\
\Rightarrow v'&=v\frac{s'}{s}\\
&=2\times\frac{5}{4}=2\text{,}5\ \text{cm/s}
\end{align}
Câu 5 (1,0 điểm). Đề và đáp án thi vào lớp 10 chuyên Lý Hải Phòng 2023
Một thanh kim loại MN cứng, đồng chất, thẳng có chiều dài $L = 0\text{,}5\ \text{m}$ và tiết diện đều $s = 4.10^{-4}\ \text{m}^2$. Thanh được treo bởi một sợi dây thẳng đứng, nhẹ, cách điện, không giãn. Điểm treo ở trung điểm của MN. Hệ thống được đặt trong vùng không gian có từ trường đều mà các đường sức từ có chiều đi từ trong ra ngoài và vuông góc với mặt phẳng hình 5. Cho dòng điện $I$ không đổi chạy qua thanh thì thấy khi cân bằng thanh nằm ngang, đồng thời lực căng dây $T$ lớn hơn trọng lượng $P$ của thanh.
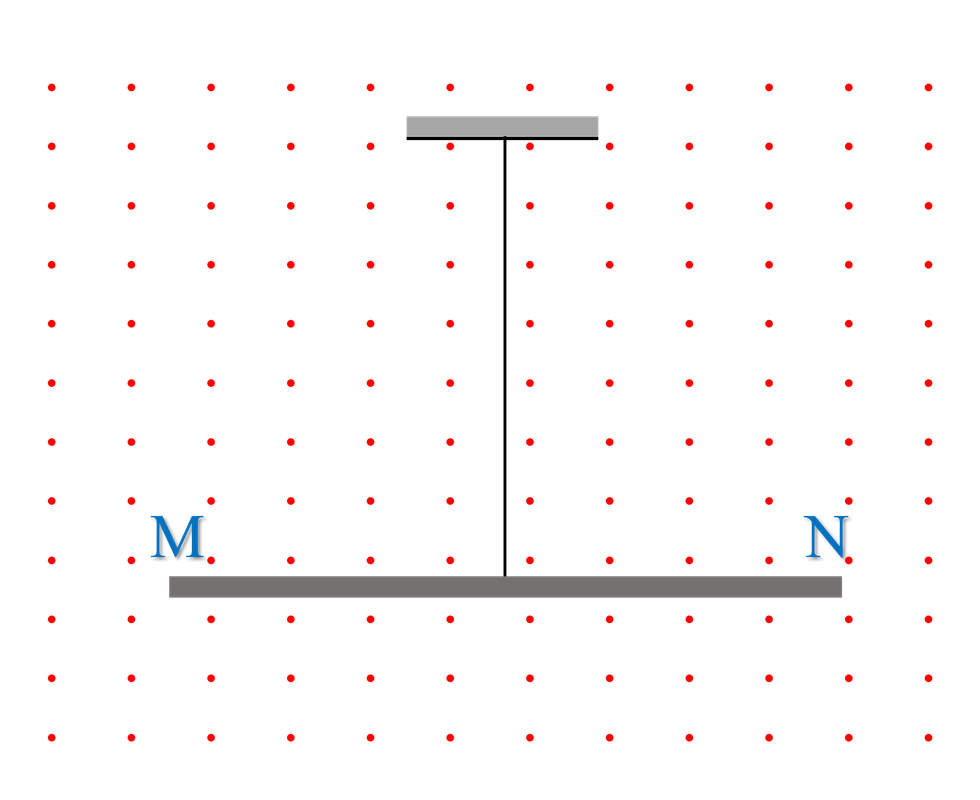
- Xác định phương, chiều lực điện từ và chiều dòng điện chạy qua thanh. Giải thích.
- Tìm độ lớn lực điện từ biết $T = 20\text{,}8\ \text{N}$ và trọng lượng riêng của thanh là $d = 89000\ \text{N/m}^3$.
1. Xác định chiều của lực từ và chiều dòng điện trong thanh MN
+ Lực điện từ đặt tai trung điểm của thanh MN, có phương vuông góc với các đường sức đồng thời vuông góc với thanh MN nên nó trùng với phương sợi dây treo.
+ Do lực căng sợi dây lớn hơn trọng lực của thanh nên suy ra lực điện từ hướng xuống.
+ Áp dụng quy tắc bàn tay trái suy ra chiều dòng điện đi từ M đến N.
2. Tính độ lớn lực điện từ $F$
Phương trình cân bằng lực:
\begin{align}
T&=P+F\\
F&=T-P\\
&=T-10dLS\\
&=20\text{,}8-89000.0\text{,}5.4.10^{-4}\\
&=3\ \text{N}
\end{align}
2 Nhận xét đề thi vào lớp 10 chuyên Lý Hải Phòng 2023
+ Nhận xét chung: Đề hơi dài, mức độ khó chiếm tỉ lệ quá cao so với các mức độ khác. Có cảm giác như thí sinh cần phải tập trung cao độ trong tất cả các câu, các ý.
+ Câu 1: Mức độ vừa phải, đã có sự tăng dần độ khó qua từng ý, tạo cho học sinh một tâm lí thoải mái khi bước vào làm bài thi.
+ Câu 2: Yêu cầu học sinh phải có kĩ năng đọc đồ thị. Qua đây, các thầy cô luyện thi chắc chắn phải bổ sung vào giáo trình của mình phần đồ thị. Câu này theo nhận định cũng khó để học sinh giải quyết đảm bảo thời gian.
+ Câu 3: Ngay ý 1 đã làm khó học sinh rồi. Ý này nên hỏi các em về dòng điện, hiệu điện thế hay công suất gì đó. Chưa kể, học sinh có biết hay không độ sáng của đèn tỉ lệ với công suất tiêu thụ? Có em đem so sánh độ sáng của đèn với cường độ dòng điện qua đèn thì sao? Ý 2 công suất lớn nhất thì học sinh đã quen, nhưng công suất nhỏ nhất lại là vấn đề khó. Đến ý 2b, c thì quả thật là khó. Theo tôi nên bỏ câu 3c.
Tóm lại đề khá hay, đáng để tham khảo.




Cảm ơn bác.Tài liệu hay để tham khảo
Trả lờiXóa