Đề thi vào lớp 10 chuyên lý Hà Tĩnh năm 2023 có lời giải chi tiết
Các kì thi do sở Giáo dục và Đào Tạo Hà Tĩnh luôn có những đề thi chất lượng, trong đó có kì thi tuyển sinh vào lớp 10 chuyên. Đề thi vào lớp 10 chuyên lý Hà Tĩnh năm 2023 cũng không ngoại lệ, rất hay và thú vị. Có lẽ do chất lượng học sinh của tỉnh Hà Tĩnh khá cao, các em rất chịu khó tìm tòi nên các đề trên mạng hay trong những quyển sách quen thuộc, các em đều đã giải hết. Điều này đòi hỏi ban ra đề của sở Giáo dục và Đào tạo Hà Tĩnh phải sáng tạo hơn trong khâu ra đề. Bài viết này xin chia sẻ cùng các bạn Đề thi vào lớp 10 chuyên lý Hà Tĩnh năm 2023 có lời giải chi tiết. Cũng lưu ý rằng, đây không phải đáp án chính thức, mà chỉ là lời giải theo chủ quan của tác giả. Hi vọng mang lại thêm một tài liệu hay cho các bạn.
1 Đề và đáp án thi vào lớp 10 chuyên Lý Hà Tĩnh 2023
Câu 1 (2,0 điểm). Đề và đáp án thi vào lớp 10 chuyên Lý Hà Tĩnh 2023
Một ô tô xuất phát từ điểm A trên sân vận động thứ nhất để đến điểm B trên sân vận động thứ hai như hình 1. Hai sân vận động được ngăn cách nhau bởi con đường thẳng (D), khoảng cách từ A đến đường (D) là $a=800\ \text{m}$, khoảng cổch từ B đến đường (D) là $b = 600\ \text{m}$, $AB=5600\ \text{m}$. Biết tốc độ của ô tô trên sân vận động thứ nhất là $v_1=30\ \text{km/h}$, trên đường (D) là $v=50\ \text{km/h}$, trên sân vận động thứ hai là $v_2=40\ \text{km/h}$.
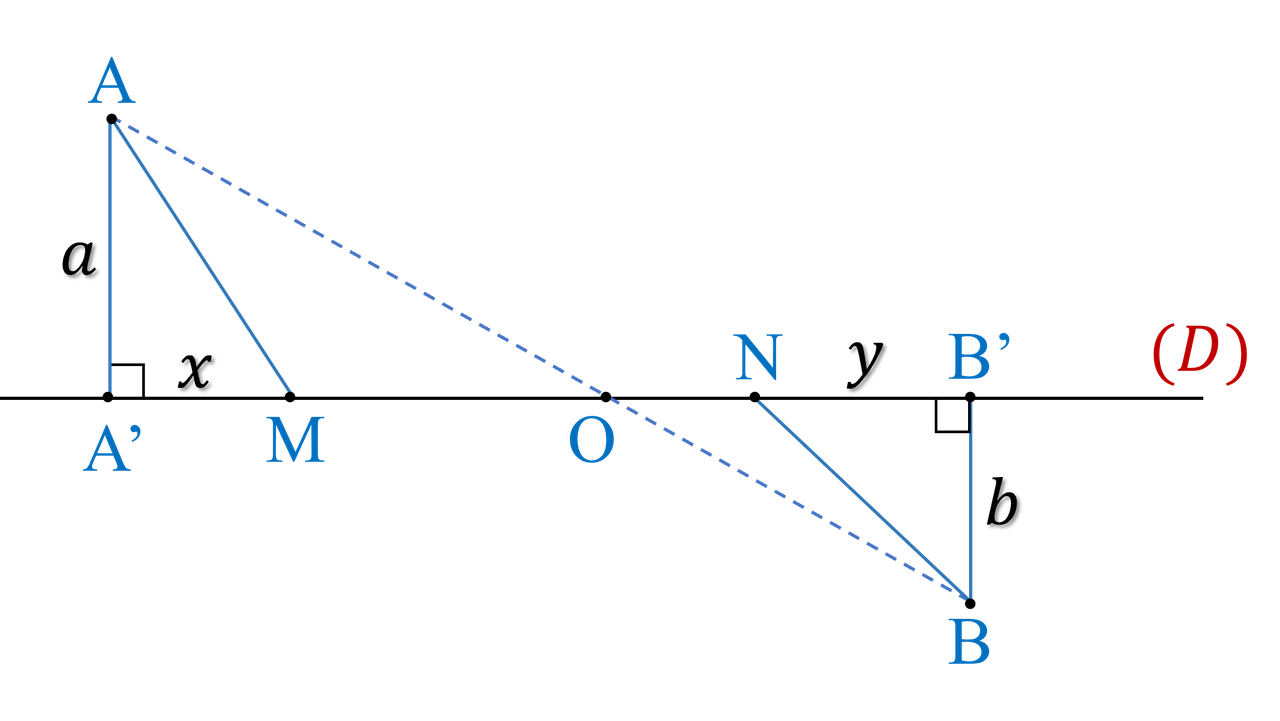
- Tính thời gian ô tô đi từ A đến B, nếu ô tô đi theo đường $AA'B'B$.
- Nếu ô tô đi theo hướng từ điềm A đến điểm M trên đường cách A' một khoảng $x$ và rời đường tại N cách B' một khoảng $y$. Tìm $x$ và $y$ để thời gian chuyển động từ A đến B là nhỏ nhất. Xác định khoảng thời gian nhỏ nhất đó.
1. Thời gian ô tô đi từ A đến B theo đường $AA'B'B$
Trước hết ta tính độ dài quãng đường từ A' đến B'
\begin{align}
s_\text{A'B'}&=\sqrt{s_\text{AB}^2-\left(a+b\right)^2}\\
&=\sqrt{5600^2-\left(800+600\right)^2}\\
&=1400\sqrt{15}\ \text{m}
\end{align}
Thời gian ô tô đi từ A đến B theo đường $AA'B'B$ là
\begin{align}
t_\text{AA'B'B}&=\frac{a}{v_1}+\frac{s_\text{A'B'}}{v}+\frac{b}{v_2}\\
&=\frac{0\text{,}8}{30}+\frac{1\text{,}4\sqrt{15}}{50}+\frac{0\text{,}6}{40}\\
&\approx 0\text{,}15\ \text{h}=9\ \text{min}
\end{align}
2. Tìm cách đi từ A đến B với thời gian nhỏ nhất
Tổng thời gian ô tô đi từ A đến B là
\begin{align}
t&=\frac{\sqrt{a^2+x^2}}{v_1}+\frac{s_\text{A'B'}-\left(x+y\right)}{v}+\frac{\sqrt{b^2+y^2}}{v_2}\\
&=\frac{v\sqrt{a^2+x^2}-v_1x}{v_1v}+\frac{v\sqrt{b^2+y^2}-v_2y}{v_2v}+\frac{s_\text{A'B'}}{v}
\end{align}
Ta đặt $A=v\sqrt{a^2+x^2}-v_1x$ và xét giá trị cực tiểu của $A$. Chuyển vế và bình phương hai vế, ta suy ra
$$
\left(v^2-v_1^2\right)x^2-2v_1Ax+v^2a^2-A^2=0
$$
Điều kiện để phương trình có nghiệm là $\Delta'\ge 0$, tức là
\begin{align}
v_1^2A^2-\left(v^2-v_1^2\right)\left(v^2a^2-A^2\right)\ge 0\\
A\ge \sqrt{\left(v^2-v_1^2\right)a^2}
\end{align}
Một cách tương tự, ta đặt $B=v\sqrt{b^2+y^2}-v_2x$ và suy ra
$$B\ge \sqrt{\left(v^2-v_2^2\right)b^2}$$
Va cuối cùng ta có
$$t\ge \frac{\sqrt{\left(v^2-v_1^2\right)a^2}}{v_1v}+\frac{\sqrt{\left(v^2-v_2^2\right)b^2}}{v_2v}+\frac{s_\text{A'B'}}{v}$$
Dấu "=" xảy ra khi
$$
x=\frac{v_1^2a^2}{v^2-v_1^2}\\
y=\frac{v_2^2a^2}{v^2-v_2^2}
$$
Thay số $s_\text{A'B'}=1\text{,}4\sqrt{15}\ \text{km}$, $a=0\text{,}8\ \text{km}$, $b=0\text{,}6\ \text{km}$, $v_1=30\ \text{km/h}$, $v_2=40\ \text{km/h}$, $v=50\ \text{km/h}$, ta được
$$
x=0\text{,}6\ \text{km}\\
y=0\text{,}8\ \text{km}\\
t_\text{min}\approx 0\text{,}1388\ \text{h}\approx8\text{,}33\ \text{min}
$$
Câu 2 (2,0 điểm). Đề và đáp án thi vào lớp 10 chuyên Lý Hà Tĩnh 2023
Một bình nóng lạnh chứa 5 lít nước, công suất tiêu thụ điện năng là $P=1500\ \text{W}$. Mùa đông nhiệt độ nước chảy vào bình nóng lạnh là $20\ \text{°C}$. Biết nhiệt dung riêng của nước là $c = 4200\ \text{J/kg.K}$, khối lượng riêng của nước là $D= 1\ \text{kg/lít}$ (coi như không đổi). Cho rằng bình nóng lạnh sử dụng đúng công suất và toàn bộ nhiệt năng do dòng điện sinh ra chỉ truyền cho nước trong bình.
- Tính thời gian bật bình nóng lạnh để nước trong bình tăng nhiệt độ từ $20\ \text{°C}$ đến $70\ \text{°C}$.
- Trong quá trình sử dụng luôn có dòng nước lạnh $20\ \text{°C}$ chảy vào bình và dòng nước nóng $70\ \text{°C}$ chảy ra khỏi bình. Tính lưu lượng nước chảy qua bình nóng lạnh (sổ lít nước chảy qua bình trong một giây) để đảm bảo được nhiệt độ ổn định như trên.
- Khi sử dụng người ta pha trộn nước $70\ \text{°C}$ chảy ra từ bình nóng lạnh (lưu lượng ở ý 2) với một vòi nước lạnh khác ở nhiệt độ $20\ \text{°C}$. Để nước ngay sau khi pha trộn có nhiệt độ $40\ \text{°C}$ thì tốc độ dòng chảy trong vòi nước lạnh là bao nhiêu? Biết tiết diện của ống nước lạnh là $S=1\text{,}2\ \text{cm}^2$.
1. Thời gian bật bình nóng lạnh
Nhiệt lượng mà dòng điện cung cấp cho $5\ \ell$ nước trong thời gian $\tau$ là $Q=P\tau$, nó còn được tính bằng công thức $Q=mc\Delta t$, tức là ta có phương trình
\begin{align}
P\tau&=mc\Delta t\\
\Rightarrow \tau&=\frac{mc\Delta t}{P}\\
&=\frac{5.4200.\left(70-20\right)}{1500}\\
&=700\ \text{s}=11\ \text{min}\ 40\ \text{s}
\end{align}
2. Lưu lượng nước chảy qua bình nóng lạnh khi sử dụng
Gọi $V_1$ là số lít nước qua bình trong 1 giây, nhiệt lượng mà phần nước này trao đổi với dòng điện là
\begin{align}
P&=V_1c\Delta t\\
V_1&=\frac{P}{c\Delta t}\\
&=\frac{1500}{4200.50}=\frac{1}{140}\ \ell\text{/s}
\end{align}
3. Tốc độ dòng nước trong ống lạnh
Gọi $v$ là tốc độ dòng nước trong ống lạnh thì thể tích nước (tính theo lít) từ ống này chảy vào bể trộn trong 1 giây là $V_2=v.S$, với $v$ tính theo $\text{dm/s}$, $S$ tính theo $\text{dm}^2$. Phương trình cân bằng nhiệt giữa $V_1\ \ell$ nước nóng $V_2\ \ell$ nước lạnh chảy vào bể trong 1 giây là
\begin{align}
V_1c\left(70-40\right)&=v.S.c\left(40-20\right)\\
v&=\frac{30V_1}{20S}\\
&=\frac{30.\frac{1}{140}}{20.1\text{,}2.10^{-2}}=\frac{25}{28}\approx 0\text{,}893\ \text{dm/s}
\end{align}
Câu 3 (2,5 điểm). Đề và đáp án thi vào lớp 10 chuyên Lý Hà Tĩnh 2023
Cho mạch điện như hình 2a. Biết nguồn điện có hiệu điện thế $U= 3\ \text{V}$, các điện trở $R_1 = 3\ \Omega$, $R_2 = 2\ \Omega$, các đèn như nhaụ đều có ghi $1\text{,}5\ \text{V} - 0\text{,}5\ \text{W}$. Ampe kế, điểm tiếp xúc và các dây nối có điện trở không đáng kể.
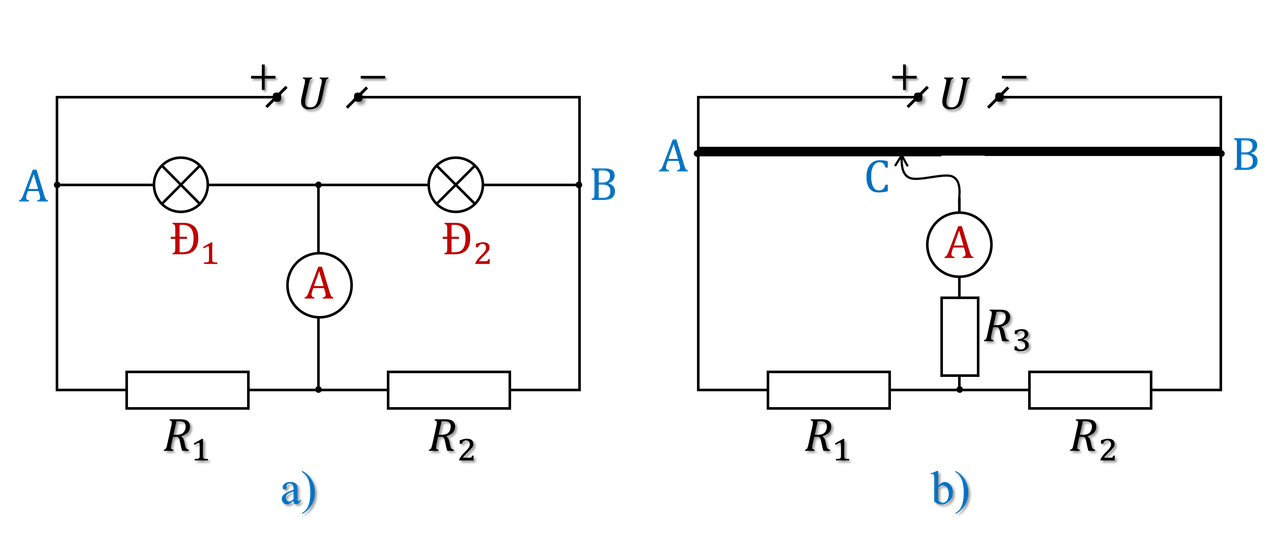
- Xác định độ sáng các bóng đèn so với bình thường và tính số chỉ của ampe kế.
- Tháo các đèn $\text{Đ}_1$ và $\text{Đ}_2$ ra và mắc vào giữa hai điểm A vầ B một thanh dẫn điện đổng chất tiết diện đều có điện trở toàn phần $R_0$. Mắc điện trở $R_3 = 2\ \Omega$ nối tiếp với ampe kế, trong đó điểm nổi C giữa ampe kế với thanh AB có thể di chuyển được và luôn tiếp xúc điện với thanh dẫn như hình 2b. Khi $R_\text{AC} = 3\ \Omega$ thì ampe kế chỉ 0. Tìm số chỉ của ampe kế khi $R_\text{AC}=1\ \Omega$.
1. Độ sáng của các đèn và số chỉ ampe kế
Điện trở và cường độ định mức của các đèn lần lượt là
\begin{align}
R_\text{Đ}&=\frac{U_\text{đ}^2}{P_\text{đ}}\\
&=\frac{1\text{,}5^2}{0\text{,}5}=4\text{,}5\ \Omega\\
I&=\frac{P_\text{đ}}{U_\text{đ}}\\
&=\frac{0\text{,}5}{1\text{,}5}=\frac{1}{3}\ \text{A}
\end{align}
Ta quy ước các dòng điện trong mạch như hình dưới đây:
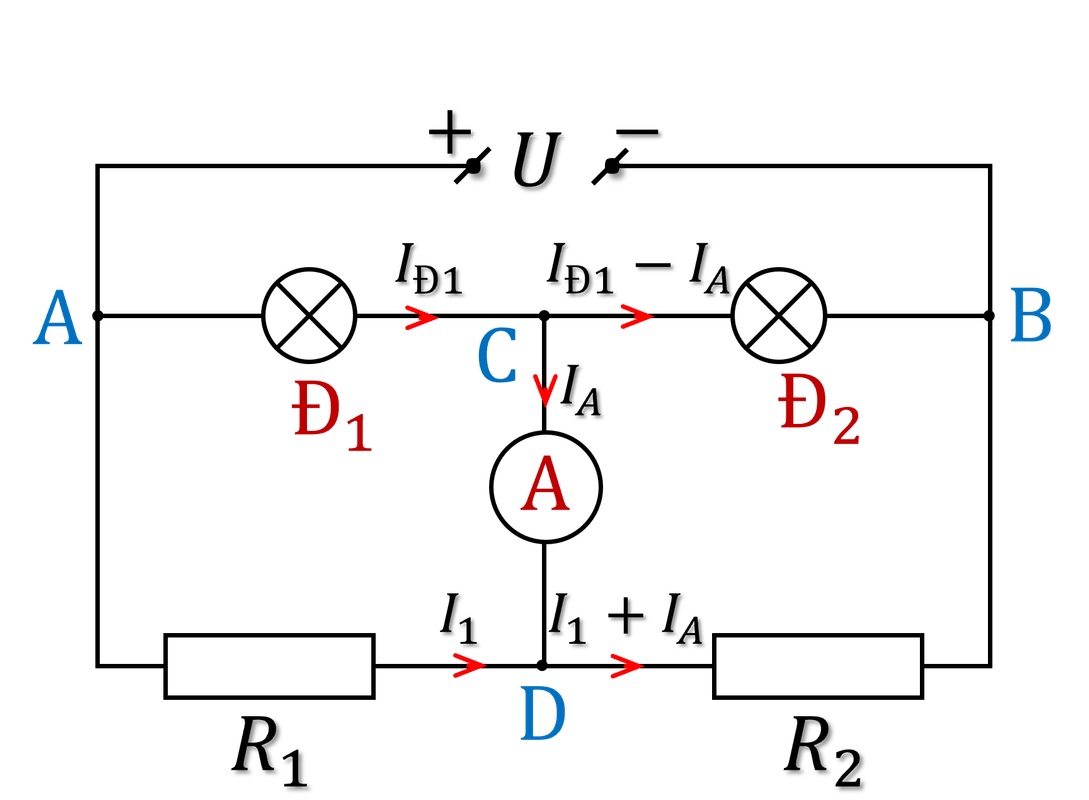
Phương trình định luật Ôm cho các đoạn mạch:
\begin{align}
U_\text{AB}&=R_\text{Đ}I_\text{Đ1}+R_\text{Đ}\left(I_\text{Đ1}-I_\text{A}\right)\\
3&=4\text{,}5I_\text{Đ1}+4\text{,}5\left(I_\text{Đ1}-I_\text{A}\right)\tag{3.1}\label{3.1}\\
U_\text{AB}&=R_1I_1+R_2\left(I_1+I_\text{A}\right)\\
3&=3I_1+2\left(I_1+I_\text{A}\right)\tag{3.2}\label{3.2}\\
U_\text{AC}&=U_\text{AD}\\
4\text{,}5I_\text{Đ1}&=3I_1\tag{3.3}\label{3.3}
\end{align}
Ta có hệ 3 phương trình bậc nhất (\ref{3.1}), (\ref{3.2}), (\ref{3.3}), (dùng máy tính Casio) giải ra ta được
$$
I_\text{Đ1}=\frac{26}{69}\approx0\text{,}377\ \text{A}\\
I_\text{A}=\frac{2}{23}\approx0\text{,}087\ \text{A}\\
I_1=\frac{13}{23}\approx0\text{,}566\ \text{A}\\
$$
Kết quả là số chỉ ampe kế $I_\text{A}=0\text{,}087\ \text{A}$, $I_\text{Đ1}\gt I_\text{đ}$ nên sáng hơn bình thường, $I_\text{Đ2}=I_\text{Đ1}-I_\text{A}=0\text{,}29\ \text{A}\lt I_\text{đ}$ nên tối hơn bình thường.
2. Tìm số chỉ ampe kế khi thay các đèn bằng thah dẫn
Khi $R_\text{AC}=3\ \Omega$ thì ampe kế chỉ 0, lúc đó mạch cầu cân bằng, ta có
\begin{align}
\frac{R_0-3}{R_2}&=\frac{3}{R_1}\\
\Rightarrow R_0&=3\left(\frac{R_1}{R_2}+1\right)\\
&=3\left(\frac{3}{2}+1\right)=7\text{,}5\ \Omega
\end{align}
Khi $R_\text{AC}=1\ \Omega$ thì $R_\text{CB}=6\text{,}5\ \Omega$. Quy ước dòng điện như trong hình dưới đây:
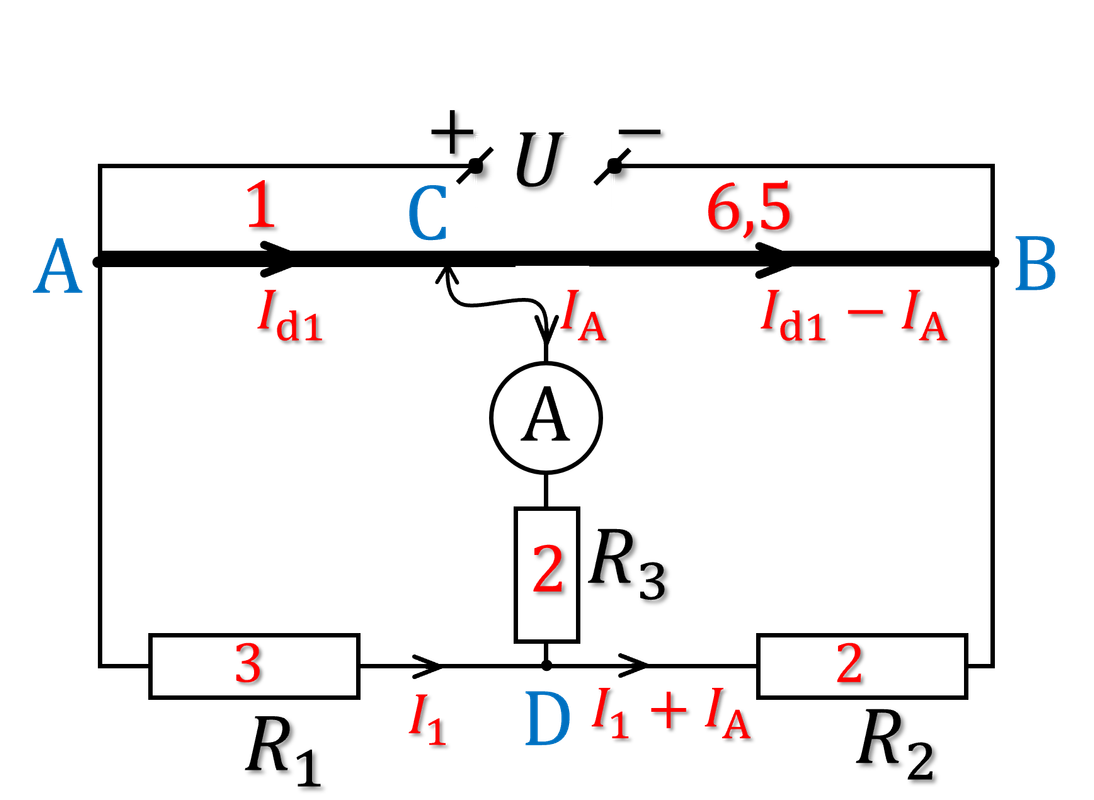
\begin{align} U_\text{AB}&=U_\text{AC}+U_\text{CB}\\ 3&=1.I_\text{d1}+6\text{,}5\left(I_\text{d1}-I_\text{A}\right)\tag{3.4}\label{3.4}\\ U_\text{AB}&=U_\text{AD}+U_\text{DB}\\ 3&=3.I_1+2\left(I_1+I_\text{A}\right)\tag{3.5}\label{3.5}\\ U_\text{AC}&=U_\text{AD}+U_\text{DC}\\ 1.I_\text{d1}&=3.I_1-2I_\text{A}\tag{3.6}\label{3.6} \end{align} Giải hệ 3 phương trình bậc nhất (\ref{3.4}), (\ref{3.5}), (\ref{3.6}) (giải bằng máy tính Casio) ta được $$ I_\text{d1}=0\text{,}698\ \text{A}\\ I_\text{A}=0\text{,}344\ \text{A}\\ I_1=0\text{,}462\ \text{A} $$ Số chỉ ampe kế là $0\text{,}344\ \text{A}$.
Câu 4 (1,5 điểm). Đề và đáp án thi vào lớp 10 chuyên Lý Hà Tĩnh 2023
1. Một dây cáp truyền tải điện có chiều dài $L$ như hình 5, phía trong ruột cồm hai dây dẫn hợp kim như nhau. Do sự cố nên hai dây dẫn bị ngắn mạch (tiếp xúc điện với nhau) tại một điểm trong dây cáp. Bỏ qua điện trở tiếp xúc.

- Xác định khoảng cách từ đầu $A_1A_2$ vị trí ngắn mạch nếu đo được điện trở giữa hai đầu $A_1A_2$ là $R_1$, giừa hai đầu $B_1B_2$ là $R_2$.
- Cho các dụng cụ gồm: Ampe kế lí tưởng, nguồn điện không đổi có hiệu điện thế $U$, các đoạn dây nối có điện trở không đáng kể. Hãy nêu phương án thí nghiệm để xác định vị trí bị ngắn mạch.
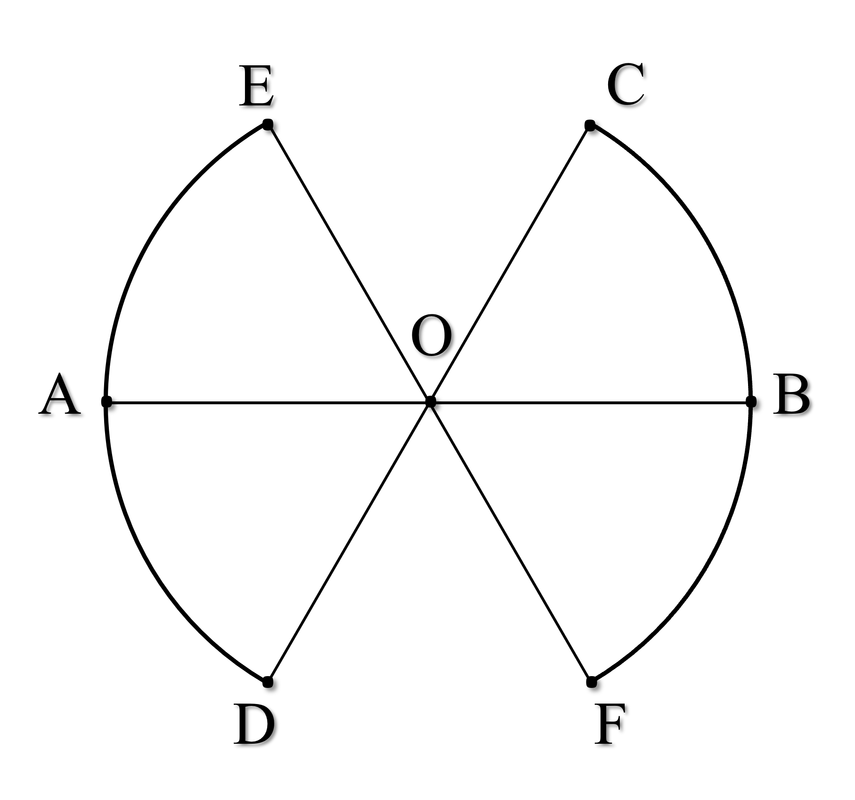
2. Cho một sợi dây dẫn làm bằng kim loại, đồng chất, dài 2 m, tiết diện tròn, đường kính 0,5 mm. Điện trở suất $\rho = 0\text{,}5.10^{-6}\ \Omega\text{m}$. Uốn sợi dây thành hình có dạng như hình 6, trong đó các đoạn dây OA, OE, OC, OB, OF, OD là các bán kính đường tròn và hợp với nhau các góc 60°, còn CBF và EAD là các cung tròn. Bỏ qua điện trở các mối hàn. Cho $\pi = 3\text{,}14$. Tính điện trở tương đương của đoạn mạch AB.
1a. Khoảng cách từ đầu $A_1A_2$ đến vị trí ngắn mạch
Gọi khoảng cách từ đầu $A_1A_2$ đến điểm ngắn mạch là $x$, $\rho$ là điện trở suất của hợp kim là lõi cáp, $S$ là tiết diện mỗi dây dẫn, thì
\begin{align}
R_1&=\frac{\rho.2x}{S}\tag{4.1}\label{4.1}\\
R_2&=\frac{\rho.2\left(L-x\right)}{S}\tag{4.2}\label{4.2}\\
\end{align}
Cộng hai phương trình (\ref{4.1}) và (\ref{4.2}) vế theo vế ta được
\begin{align}
R_1+R_2=\frac{\rho.2L}{S}\tag{4.3}\label{4.3}
\end{align}
Chia (\ref{4.1}) cho (\ref{4.3}) vế theo vế ta được
\begin{align}
x=\frac{R_1}{R_1+R_2}\tag{4.4}\label{4.4}
\end{align}
1b. Phương án thực hành tìm vị trí ngắn mạch
Theo (\ref{4.4}) thì ta chỉ cần đo được điện trở $R_1$ giữa hai đầu $A_1A_2$ và $R_2$ giữa hai điểm $B_1B_2$. Với nguồn điện có hiệu điện thế $U$ đã biết và ampe kế lí tưởng, ta làm như sau:
+ Nối một đầu ampe kế với cực dương nguồn điện, đầu còn lại của ampe kế nối với đầu $A_1$, nối đầu $A_2$ với cực âm của nguồn điện.
+ Đọc số chỉ ampe kế, ta đặt là $I_1$.
+ Tính điện trở $R_1$
$$
R_1=\frac{U}{I_1}
$$
+ Nối một đầu ampe kế với cực dương nguồn điện, đầu còn lại của ampe kế nối với đầu $B_1$, nối đầu $B_2$ với cực âm của nguồn điện.
+ Đọc số chỉ ampe kế, ta đặt là $I_2$.
+ Tính điện trở $R_2$
$$
R_2=\frac{U}{I_2}
$$
+ Áp dụng (\ref{4.4}) ta xác định được khoảng cách $x$ từ đầu $A_1A_2$ đến điểm ngắn mạch:
\begin{align}
x=\frac{\frac{U}{I_1}}{\frac{U}{I_1}+\frac{U}{I_2}}=\frac{I_2}{I_1+I_2}
\end{align}
2. Tính điện trở tương đương
Gọi chiều dài các đoạn thẳng (bán kính) là $r$ thì độ dài các cung tròn ($60^\text{o}$) là $c=\frac{1}{6}2\pi r$. Tổng chiều dài dây bằng 2 m, ta có
\begin{align}
6r+4\times \frac{1}{6}2\pi r&=2\\
r&=\frac{3}{9+2\pi}\\
R_\text{AB}&=2R_\text{AO}\\
&=2\frac{\rho}{\pi\frac{d^2}{4}}\frac{\frac{c+r}{2}.r}{\frac{c+r}{2}+r}\\
&=\frac{8\left(3+\pi\right)r\rho}{\pi d^2\left(9+\pi\right)}
\end{align}
Thay số vào ta tính được
$$
R_\text{AB}=0\text{,}5\ \Omega
$$
Câu 5 (2,0 điểm). Đề và đáp án thi vào lớp 10 chuyên Lý Hà Tĩnh 2023
Một vật sáng AB có dạng đoạn thẳng được đặt vuông góc với trục chính của một thấu kính hội tụ có tiêu cự $f$, điểm B nằm trên trục chính thấu kính.
- Tại vị trí vật AB cho ảnh A'B' ngược chiều, cao bằng $\frac{1}{2}$ vật và cách vật 90 cm. Bằng phép vẽ, hãy xác định vị trí đặt thấu kính và tính tiêu cự $f$.
- Gọi $d$ là khoảng cách từ vật AB đến thấu kính, $h$ là độ cao của vật AB, $h'$ là độ cao của ảnh A'B'. Dịch chuyển vật dọc theo trục chính của thấu kính sao cho ảnh và vật luôn ngược chiều nhau. Hãy vẽ đồ thị mô tả sự phụ thuộc của $\frac{h}{h'}$ theo $d$.
1. Dùng phép vẽ xác định vị trí thấu kính
Ảnh ngược chiều vật là ảnh thật. Ta vẽ theo các bước sau:
Vẽ trục chính là một đường thẳng nằm ngang, vẽ vật và ảnh ngược chiều, cách nhau 90 cm, B và B' nằm trên trục chính, $AB=2A'B'$.
Vẽ đường thẳng từ A đi qua A', đường thẳng này là một tia sáng đi qua quang tâm O nên giao điểm của nó với trục chính là quang tâm O của thấu kính.
Vẽ thấu kính hội tụ vuông góc với trục chính tại O.
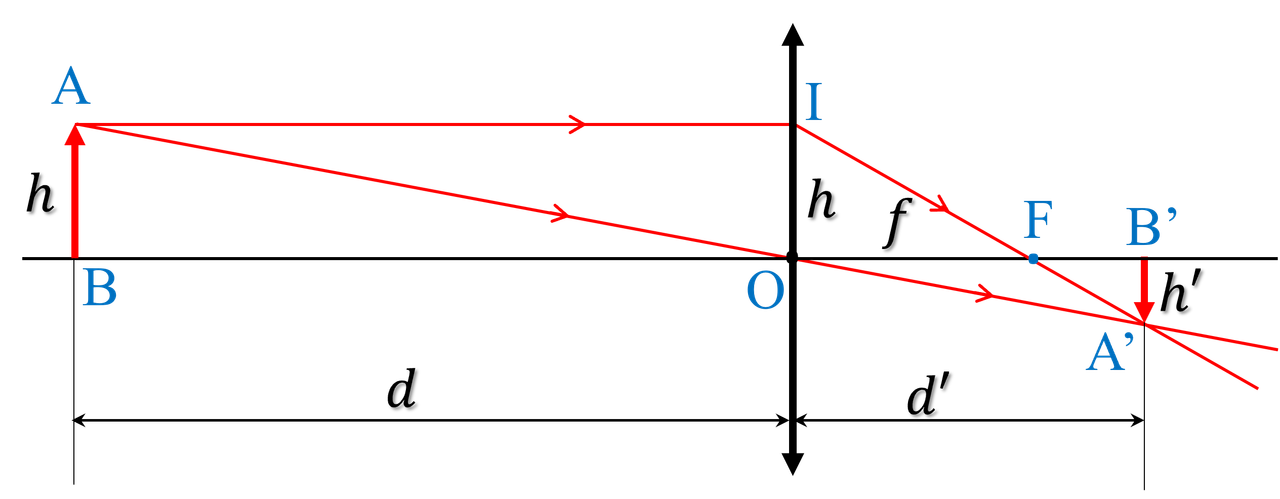
Xét các tam giác đồng dạng trong hình 7 ta có
\begin{align}
\frac{h}{h'}=\frac{d}{d'}=\frac{f}{d'-f}=\frac{d-f}{f}\tag{5.1}\label{5.1}
\end{align}
Theo bài ra thì $\frac{h}{h'}=2$ và $d'=90-d$, thay vào (\ref{5.1}) ta được
\begin{align}
2&=\frac{d}{90-d}\\
d&=60\ \text{cm}
\end{align}
Thay trở lại (\ref{5.1}) ta được
\begin{align}
2&=\frac{60-f}{f}\\
\Rightarrow f&=20\ \text{cm}
\end{align}
2. Vẽ đồ thị biểu diễn sự phụ thuộc của $\frac{h}{h'}$ theo $d$
Ta sử dụng (\ref{5.1}) với $f=20\ \text{cm}$, đặt $y=\frac{h}{h'}$ và $x=d$, đây là hàm số bậc nhất:
$$
y=\frac{1}{20}x-1
$$
Đồ thị của hàm số:
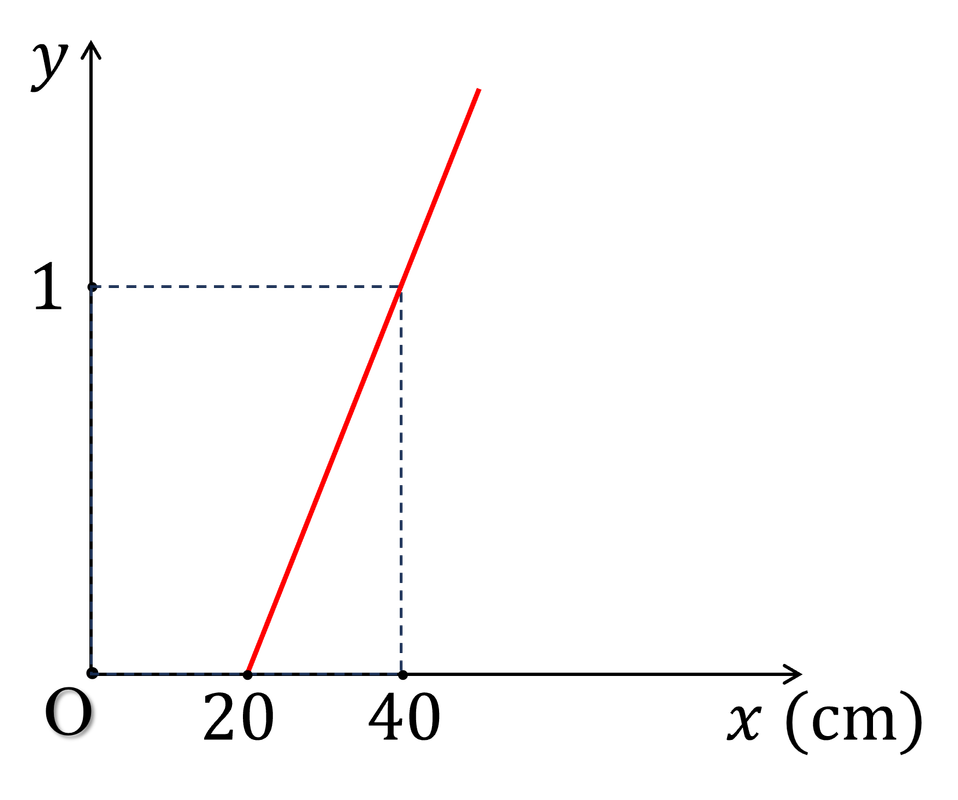
Trong đó, để ảnh luôn ngược chiều vật (ảnh thật) thì vật luôn nằm ngoài tiêu cự của thấu kính, tức là $x\gt 20\ \text{cm}$.
2 Nhận xét đề thi vào lớp 10 chuyên Lý Hà Tĩnh 2023
+ Cái nhìn đầu tiên: Đề nhìn có vẻ dài, các hình vẽ lạ so với các bài toán quen thuộc mà học sinh THCS thường được luyện, nên các em sẽ có phần hoang mang. Tuy nhiên xu hướng ra đề bây giờ nên như thế này, đừng mãi loanh quanh luyện đi luyện lại các bài toán quen thuộc, học sinh thi điểm cao nhưng lên THPT thì không có khả năng sáng tạo, không phát triển được.
+ Mức độ của đề: Khá cao so với đa số học sinh trong cả nước. Nhưng đối với học sinh Hà Tĩnh thì chắc là phù hợp.
+ Phân bố các mức độ từ nhận biết đến vận dụng cao: Có vẻ như các mức từ nhận biết đến thông hiểu không có trong đề thi này. Riêng ý 2 câu 1 thì ngang với đề thi HSG quốc gia.
+ Liệu có đảm bảo thời lượng? Nếu học sinh chưa bao giờ gặp thì chắc không học sinh nào làm kịp thời gian (kể cả giáo viên giỏi).
Tóm lại đề khá hay, đáng để tham khảo.




Không có nhận xét nào: